高中物理解题小技巧（9）——物体运动过程中的临界态问题

物体运动过程中的临界态问题

物体的运动状态是其初始状态和所受合力作用的结果。

因此，物体受力情况发生变化，必然引起物体运动状态的变化。

物体的运动状态由一种情况变到另一种情况时，往往存在一个特殊点，就是物体从一种运动形式转变为另一种运动形式的分界点，它起到运动过程中的承上启下作用，我们把它叫临界点，物体所处的这个状态，我们把它叫临界态。

这个特殊状态存在着力的特殊性，运动的物理量（位移、速度、加速度、时间）的特殊性，能量、动量的特殊性等等。

不同的运动状态变化具有不同的特殊性，若能在分析物体运动状态变化的过程中，抓住主要矛盾，分析清楚特殊性，就是找到了解决问题的关键。

例1：质量为1千克的物体，受到一个恒为3牛顿的水平力的作用，由静止开始在光滑的水平面上运动，经3秒钟后运动进入摩擦系数为0.4的粗糙水平面上，求该物体从静止开始经15秒钟通过的位移是多少？

（g取10米/秒²）

解：物体的初始速度为0，

物体的受力情况，

在光滑平面上运动时，

水平方向，

受到一个恒为F=3牛顿的水平力的作用，

方向与运动方向相同，

经3秒钟运动进入摩擦系数为0.4的粗糙水平面后

水平方向，

除受到3牛顿的水平作用力以外，

还受到与运动方向相反的滑动摩擦力，

大小：f=μmg=0.4×1×10牛=4牛

f= 4牛＞F=3牛

由物体的初始速度为0和牛顿第二定律可知，

物体运动过程变化是：

静止→匀加速运动→匀减速运动→静止

其中从光滑水平面进入粗糙水平面和由匀减速到静止是变化的特殊点。

设物体加速运动时候的加速度a₁，

做减速运动时候的加速a₂，

由牛顿第二定律可知，

a₁=F/m

=3/1米/秒²

=3米/秒²

a₂=(F—μmg)/m

=（3－4）/1米/秒²

= —1米/秒²

第一个特殊点：

V₁=a₁t₁

=3·3米/秒

=9米/秒

第二个特殊点：

0= V₁+ a₂t₂ 带入数据，

∴ t₂=9秒

表明物体从匀减速运动变为静止的时刻不是15秒末而是12秒末

即物体由开始运动到静止所用的时间是12秒

∴ S=S₁+S₂

=（1/2）a₁t1₁+V₁t₂-（1/2）a₂t₂²

带入数据得，

S=54米

此题中，

第1个关键点的末速度是下一段运动的初速度，

第2个关键点的分析，可以知道物体运动的总时间不是15秒，是12秒，其中有3秒物体已经静止了。

例2：用长L的细线悬挂质量为m的小球，线能承受的最大拉力T=1.5mg，现将线与球拉直到水平位置，然后放开，运动中因细线断裂小球落地点恰好在悬点的正下方，求小球原处离地多高？（如图所示）

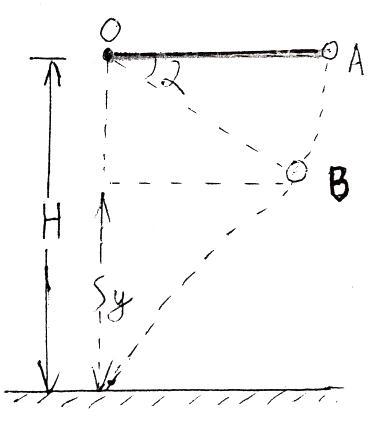
例2

解：设小球运动到B点时，细线断裂，

B点把前面的圆周运动与后面的抛物运动联系在一起

物体运动的B点是临界点，

设此时细线与水平方向所成的夹角为α角，

此处物体的速度为VB

细绳的拉力T

在B点：

小球做圆周运动：

有：T-mgsinα=mVB²g/L

又 T=1.5mg (特殊性)

∴ VB²=1.5gL-Lgsinα (1)

A—>B过程

机械能守恒

mgLsinα=（1/2） mVB²

即VB²=2gLsinα (2)

联立(1)和(2)得：3gLsinα=1.5gL

∴ sinα=1/2

α=30º

∴ VB=√(gL)

细线断后：

小球B做斜下抛运动。

运动如图：

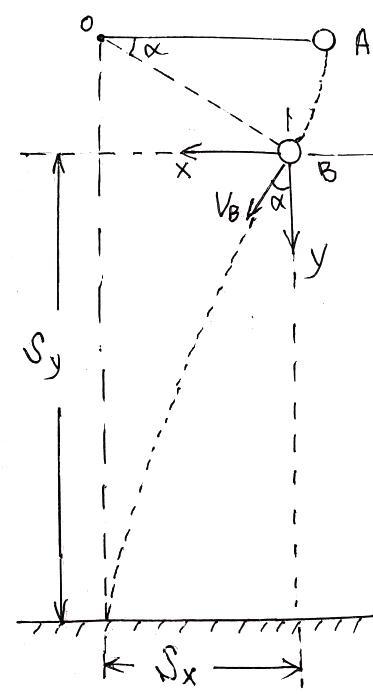
例2分析图

将物体的运动分解成水平X方向和竖直Y方向，

水平方向，

速度：大小 VX =VBsinα

=（1/2）√(gL)

方向水平向左，

加速度为0，

竖直方向，

速度： 大小 Vy =VBcosα

= （√3gL）/2

方向竖直向下，

加速度大小为g，

方向竖直向下，

∴ S X = VXt=(1/2 ) √(gL) t

由分析图可知，

S X =Lcos30º

∴ t=√(3L/g)

又 S y =VYt+（1/2）gt²

带入数据得，

S y = 3L

∴ H= S y+Lsin30º

带入数据，得

H=3.5L

例3：如图，在互相垂直的匀强磁场和匀强电场中，放一光滑足够长的绝缘斜面，倾角为30°，并固定在水平面上，磁感应在强度B方向垂直于纸面向外，电场强度为E，方向竖直向上，有一质量为m，带电量为+q的小球静止在斜面顶端，这时小球对斜面的正压力恰好为零。若迅速把电场方向改为竖直向下时，小球能在斜面上滑行多远？

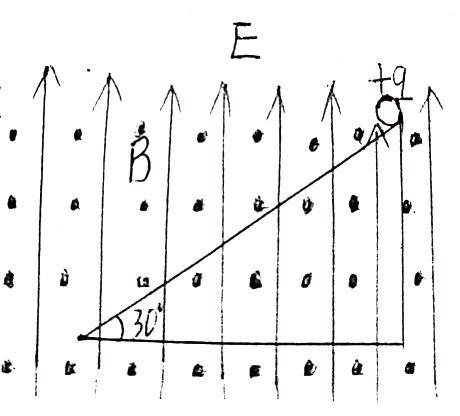
例2

解：当电场方向竖直向上时，

小球处于静止状态，

此时磁场力为0，

电场力大小为qE，方向竖直向上，

有：qE=mg

当电场方向竖直向下时，

电场力大小为qE，方向竖直向下，

小球沿斜面向下作匀加速直线运动

此过程中：

小球下滑速度在逐渐增大，

小球受的洛仑兹力也在增大，方向如图

斜面对小球的支持力在逐渐减小，

当小球下滑速度增大到某一值Vt时，

斜面对小球的支持为零（这是临界点）

此时小球开始离开斜面。

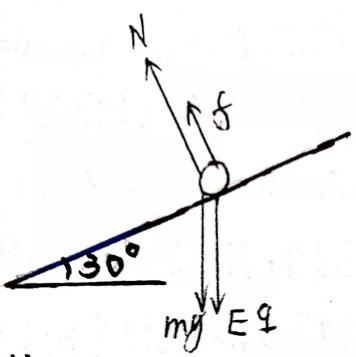
例2分析图

垂直斜面方向：

∵ f+N=(mg+Eq)cosα

又 f=BqV

当V=Vt 时 N=0

∴ BqVt=(mg+Eq)cosα

Vt=2mg cosα/（qB）

沿斜面方向上，

由牛顿第二定律：

(mg+Eq)sinα=ma

∴ a=2gsina

又（Vt）² =2aS

∴ S=（Vt）²/（2a）

=3gm²/2q²B²

小球能在斜面上最远滑行 3gm²/2q²B²

从这三个例子中可以看到，临界点是解决这些问题中的关键，找到关键点的物理量特征，就能解决问题了。