物体受力分析和运动过程的分解法(隔离法)和整体法
在分析物体的受力情况时,经常用分解法即隔离法,把多个物体(或一个物体)分解成几个物体(或几个部分),各个物体和其它物体的联系用力来表示,这种方法较复杂,优点是能显示各个物体的受力情况,能求出各物体之间的相互作用力。
有时不需要求物体之间的作用力,将几个物体作为一个整体或一个系统,只求整体的效果,这时采用整体法分析往往事半功倍。
物体的运动过程,也可以分解成几个阶段,或者一个整体来看待。
例1. 如图,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱和杆的质量为M,环的质量为m。已知环沿着杆加速下滑,环与杆的摩擦力的大小为f,则此时箱对地面的压力:
A、等于Mg
B、等于(M+m)g
C、等于Mg+f
D、等于(M+m)g-f
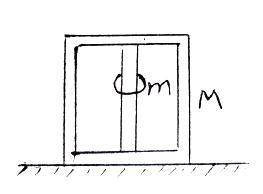
例1
解:求箱子受地面的支持力。
因这时环在竖直杆上做加速运动,
而木箱处于静止状态,不能把环和木箱作为一个整体。
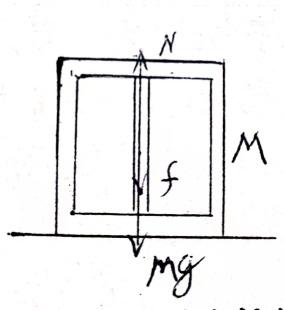
例1分析图
只能用分解法,
对于木箱的受力情况如图。
这时的f表征了环的存在。
Mg和N表征了地球的存在,
由于木箱平衡,则:
N=Mg+f
地面对木箱的支持力与木箱对地而后压力是一对作用力和反作用力,
∴ 箱对地面的压力大小为Mg+f
例2:如图,滑轮及绳子质量和摩擦力都不计,人重G1,平板均匀重G2,AB长为L,A、B距左右端长度相同,要使平板处于平衡状态,则:
(1) 人用多大的力拉绳子?
(2) 人对板的压力多大?
(3) 人应站在何处?
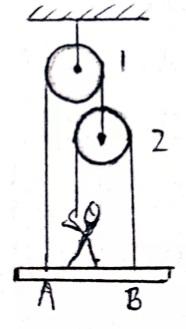
例2
解法一:用分解法分析:
人、2轮及木板的受力情况如图:
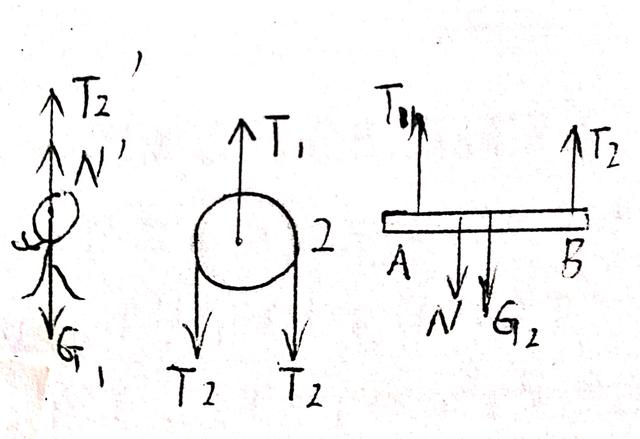
例 2 人、2轮及木板的受力情况如图
∵ 各物体都处于平衡状态,
∴ 对人:N'=G₁-T₂'
对2轮:T₁=2T₂
对木板:T₁+T₂=N+G₂
又牛顿第三定律:
T₂'=T₂
N'=N
各式联立各式解得:
(1)T₂=(G₁+G₂)/4
人用(G₁+G₂)/4的力拉绳子
(2)N=(3G₁+G₂)/4
人对木板的压力N=(3G₁+G₂)/4<人的重力G₁
(3)设人距A为X,以A为转动轴,
木板处于平衡状态,对木板有:
N·X+G₂·(L/2)=T₂·L
代入(1)中求得的T₂和N数据,得:
X=(G₁-G₂)·L/(3G₁-G₂)
从以上两例中可以看出,分解法的关键就是单独分析每一个物体,再用物理规律(可能是平衡规律、牛顿第二定律)。
解法二:用整体法:
如上面的例2用整体法解。
解:因各物体都处于静止状态(即状态相同)
(1) 把人和木板作为一体受力如图,
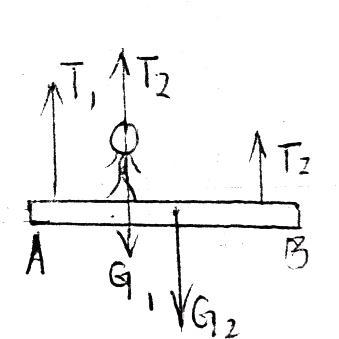
例2 木板受力分析如图
物体平衡则有:
G₁+G₂=T₁+2T₂
又 T₁=2T₂
∴T₂=(G₁+G₂)/4
(2) 人对板的压力多大?
必须用分解法同上
(3) 把人和木板作为一体,
设人距A为X,
以A为转动轴:
T₂·L+T₂·X=G₂·(L/2)+G₁·X
得
X=(G₁-G₂)·L/(3G₁-G₂)
例3:在场强为E,竖直向下的匀强电场中,有两个质量均为m的带电小球,电量分别是+2q和-q,两小球用长为L的绝缘细线相连(L远大于小球半径),另用绝缘细线系住带正电的小球悬挂于O点而处于平衡状态,如图,重力加速度为g,细线对悬点O的作用力等于多少?
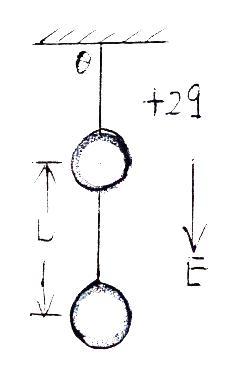
例3
解法一:因两带电小球都处于平衡状态,
所以可将它们作为一个整体,
它们之间的相互作用不用考虑。
整体共受三个力的作用:
绝缘细线向上的拉力T,
电场力(2Eq-Eq)方向向下,
总重力2mg方向向下,
整体处于平衡状态,
∴ T=(2Eq-Eq)+2mg
T=Eq+2mg
解法二:若用隔离法
分析力如图:
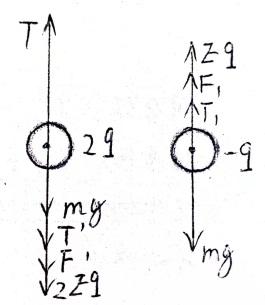
例3 受力分析图,
F₁、F'为 两电荷之间的库伦力,
T₁、T'为 两电荷之间绝缘细线的拉力,
两电荷都处于平衡状态,所以:
对+2q有T=mg+2Eq+T'+F'
对-q有:Eq+F₁+T₁=mg
由牛顿第三定律有:
F₁=F'
T₁=T'
联立得:T=Eq+2mg。
例4.密度为0.6×10³千克/米³,质量为0.12千克的木球,从离水面高10米处自由落下,若空气阻力为木球重力的1/5,水的阻力为木球重力的1/3,木球能落入水中多深处?
解:不考虑具体运动过程,只考虑整体运动,
从出发到水中静止状态,
各物理量分析如图所示,
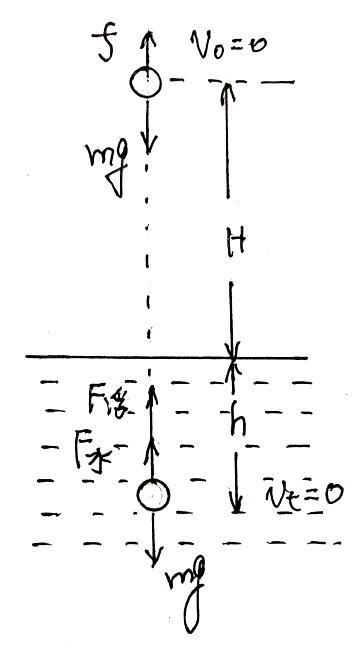
例4过程分析图
则有初状态动能为零,末状态也是动能为零,
由动能定理:
mg(H+h)-fH-(F浮+F水)h=m(v₂)²/2-m(v₁)²/2
又F浮=ρ水·g·V=ρ水·g·m/ρ木
代入数据:
得h=8米
从以上的各例题分析中可以知道,分解法和整体法各有优缺点,可以用在物体的受力分析中,也可以用在物体的运动过程中,是物理分析问题的一个基本方法。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论