高中物理解题小技巧（6）——灵活运用物体重心

灵活运用物体重心

重力是一种彻体力，即物体的每个部分都受到地球的引力作用，我们把重心看成重力的作用点，是从力的作用效果上来看，重力作用在这一点上对物体产生的效果和重力作用在所有的点上产生的效果是相同的，这是一种解决问题的等效方法，所以有的时候物体的重心可以不在物体上。

因此，只要作用的效果相同，有时可以用物体"合重心"的方法，有时又可用物体各部分的重心。

灵活的运用物体的重心，会使复杂的问题简单化。

例1． 图为重量是G的均匀等边直角尺ACO（每边厚度，宽度不计），一端用不计摩擦的铰链与墙连接，要使直尺如图（OC边水平）保持平衡，应在A点加一水平力F，则F的大小为多少？

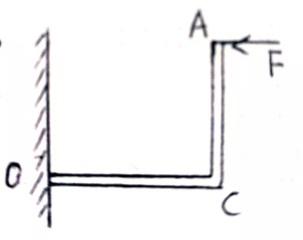
例1

解法一：用物体各部分的重心

可将直尺受的重力分为两部分，AC和CO

AC受重力G/2，作用点为E（AC的中点）

CO受重力G/2，作用点为D（CO的中点），

等边直角处于平衡状态，

以O点为轴，物体合力矩为零，则：

设AC=CO=L，

（G/2）·（L/2）+（G/2）·L=F·L

∴F=3G/4

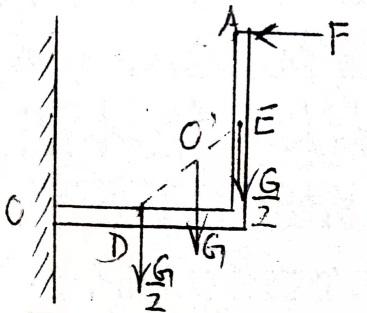
例1分析图

解法二：用物体的"合重心"，

将直尺做为一个整体，

重心在O′且在ED的中点

（1、因为物体和重心的概念是一个力的作用效果，

所以重心可以不在物体上，

2、因为是均匀等边直角尺，所以重心O′在ED的中点）

等边直角处于平衡状态，

以O点为轴，合力矩为零，则

G·3L/4=F·L

∴F=3G/4

例2：图中A、B是两块完全相同的均匀长方形砖块，长为L，有一定的厚度，叠放在一起，砖块A相对于B砖块右端伸出L/4的长度。B砖块放在水平桌面上，砖块的端面与桌边平行，为保持两砖块都不翻倒，B砖块伸出桌边的长度X的最大值为多少？

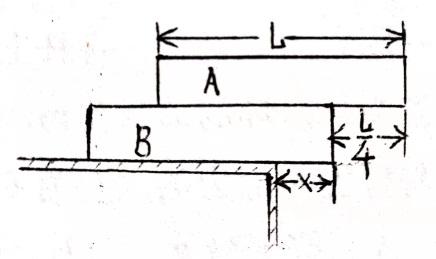
例2

解：为保持两砖块都不翻倒，B砖块伸出桌边最长时，

B受水平桌面的压力都集中在O′点，且O′点为

固定转动轴，设一块砖块的重量为G，

方法一：A、B砖块的重心分别为O ₁、O ₂，

距O′的水平距离分别为a、b，

由示意图分析可知

a+b=L/4（1）

使A、B都平衡，

B砖块伸出桌边的长度X最大

应有重心O′点在水平桌面边的正上方，

则有G·a=G·b，

∴ a=b （2）

（1）和（2）联立可解得：

a=b=L/8，

那么：X=（L/8+L/2）-L/4=3L/8

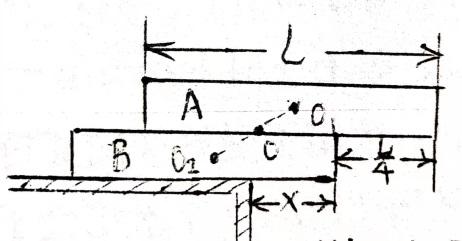
例2分析图

方法二：若将A、B合为一体看，则重心为O，

若使A、B平衡，B砖块伸出桌边最长时有：

O和O'在一条竖直线上。

由于整体对称，则O在中点，

即距左右两端都有为（L/4+L）/2=5L/8，

∴X=5L/8-L/4=3L/8

例3：如图，将水槽支于O点，当木块A浮在右边时恰好平衡，则：

A：用手压A稍为下沉，右端下倾。

B：用手压A稍为下沉，左端下倾。

C：A向左漂移，水槽仍平衡。

D：A向左漂移，水槽左端下倾。

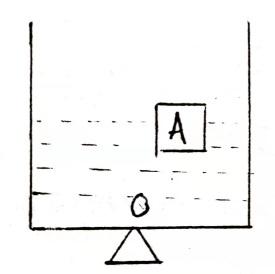
例3

解：（1）将容器、水和木块A合成一体考虑，

开始系统处于平衡状态，

物体只受重力和O点的支持力，

由二力平衡知识可知，

整体的重心一定在O点的正上方，

即支持力和重力大小相等方向相反，作用在一条直线，

当用手压木块A稍微下沉时，

在木块A施加了一个力，相当于a的重量增加了，物体会有下沉，同时木块A下沉排开的水移到了左面，其状态与原来是相同的。

物体的重心位置没有变化，

因此水槽仍然平衡

（2）将容器、水和木块A看成一体，

当木块A向左漂移时，

相当于木块A排开的这部分水在移动，

容器、水和木块A的重心没有发生变化，

因此水槽仍然保持平衡，

由前面的例题分析可知，物质的重心是一种等效的方法，有时看整体的重心，有时看部分的重心，目的都是为了解决问题的简便，熟练掌握还要在习题中逐渐体会。