用牛顿第二定律分析物体运动过程
物体受力情况和物体的初始状态决定物体的运动状态,物体的运动状态反映物体受力情况,它们的关系是:
研究对象 → F →F=ma → a →(V₂-V₁)/t → V → 运动状态
研究对象← F ←F=ma ← a ← (V₂-V₁)/t ← V← 运动状态
物体做直线运动:
当物体的初速度V0与物体的合外力方向在一条直线上时,物体做直线运动。
方向相同做加速;方向相反做减速。
物体做曲线运动:
当物体的初速度V0与物体的合外力方向不在一条直线上时,物体做曲线运动。
匀速运动:
物体初速度不为零,当物体所受合力为零时,物体做匀速运动,
匀变速运动:
当物体所受合外力恒定时,物体做匀变速运动。
几种常见运动的受力特点:
1、匀速直线运动:合外力为零:ΣF=0。
2、匀变速直线运动:ΣF=恒定,且初速度V0方向与ΣF在一直线上,
V0与F方向相同加速,方向相反减速。
特殊:自由落体,竖直上抛。
3、简谐振动:F= -kx
4、平抛运动:ΣF=mg,与V0成90°。
5、圆周运动:ΣF的方向总与V成90°(匀速圆周)。
6、行星(或卫星)运动:万有引力F=GM₁M₂/r ²。
例1:质量m=2.0千克的小铁块静止于水平导轨AB的A端,导轨及支架ABCD的形状及尺寸如图,它只能绕通过支架D点的垂直于纸面的水平轴转动,其重心在图中的O点,质量M=4.0千克,现用一细线沿导轨拉铁块,拉力F=12牛,铁块和导轨之间的摩擦系数μ=0.5,重力加速度g=10米/秒²,从铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
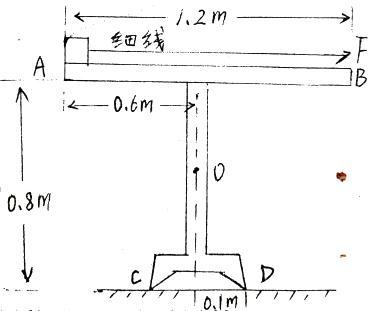
例1
解:分析导轨的情况:
导轨刚要不能维持平衡时,C端受的力为零(临界状态),
此时导轨(及支架)受四个力:
滑块对导轨的压力N=mg,竖直向下;
滑块对导轨的摩擦力f=μmg=10牛,方向向右;
重力Mg作用点O,方向竖直向下;
轴作用于D端的力。
设此时铁块走过路程S,
根据有轴物体平衡条件及图中尺寸,
有:Mg·0.1+mg(0.7-s)=f·0.8
代入数据得S=0.5米
分析铁块的情况:
受到拉力F=12牛,水平向右,
受到摩擦力f=10牛,水平向左,
由牛顿第二定律得
F-f=ma
12-10=2a
得a=1米/秒²
由s=at²/2
代入数据,得t= 1.0秒
从铁块运动时起,导轨(及支架)能保持静止的最长时间是1.0秒
此题的基本思路判断:受力情况→物体运动状态。
例2:如图,倾角为θ的光滑斜面,上端系有一劲强系数为K的轻质弹簧,弹簧的下端系有一个质量为m的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变,当挡板以加速a(a<g sinθ)沿斜面向下做匀加速运动时,
问:(1)球与挡板A开始分离时所经历的时间。
(2)球的速度达到最大时所经历的路程。(设斜面足够长)
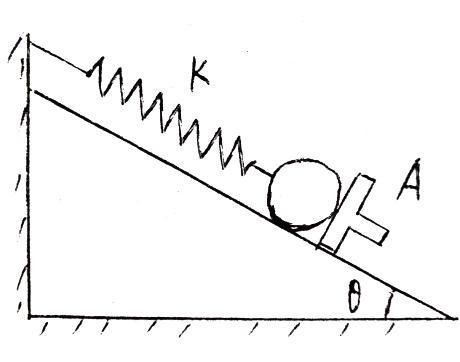
例2
解:开始小球受力如图,且有沿斜面方向:
mg sinθ-kx-N=ma
随着位移增大,kx增大,N减小
当N=0时,开始分离(临界态),
∴x=(mg sinθ-ma)/k
又因为分离前小球的运动情况与挡板相同,
小球合外力恒定,且以a做匀加速运动。
∴x=(1/2)at²
t=√(2(mg sinθ-ma)/ka)
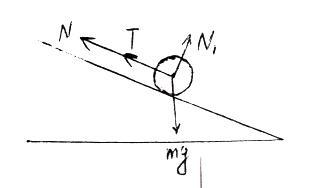
例2受力分析
分离后小球沿斜面方向只受到两个力的作用,
重力的分力,大小mg sinθ,方向沿斜面向下,
弹簧的拉力,大小kx,方向沿斜面向上,
球与挡板A开始分离的时刻(a<g sinθ)
mg sinθ>kx
小球此时的初速度沿斜面向下,合力方向沿斜面向下,
即 小球沿斜面向下做加速运动,
弹簧伸长量x增加,弹力kx增大,
小球所受的合力减小,但方向没变,
小球的加速度减小,方向也没变,
小球做加速度减小的加速运动,
当x增大到
mg sinθ=kx 时(临界状态)
a=0,
v达最大
此后小球开始做减速运动。
∴当速度最大时,mg sinθ=kx
x= mg sinθ/k
此过程可以用下面的逻辑过程表示,
由mg sinθ>kx
→做加速向下滑
→x增大
→kx增大
→(mg sinθ-kx)减小
→a减小,但方向向下
→小球做加速度减小的加速运动
→x增大到mg sinθ-kx=0时 a=0,v达最大
→开始做减速运动。
以上两个例子,都是根据物体的受力情况,应用牛顿第二定律,分析研究物体运动情况的例子。牛顿第二定律的应用,还有另外一个方面,就是根据物体的运动情况和牛顿第二定律,分析计算得出物体受力的情况。
物体受力情况和物体的运动状况关系是要熟练掌握的基本功。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论