高中物理解题小技巧（1）——物体平衡状态变化时的受力分析方法

物体处于静止状态时有共点力或合力矩为零的条件，一般容易分析。若物体在原有状态的基础上，由于某些条件发生变化，又处于另一种静止状态，由此引起其它物理量（比如力的大小、方向等）发生变化。判断这些物理量变化的情况是经常遇到的。在分析这样问题时，关键要抓住哪些量变化，哪些量不变化。下面举几个常用的方法：

（1）极端法：

找出发生变化的极端位置或特殊位置，分析物理量的变化趋势，从而判断整体的变化趋势。

例1：半径为r，重量为G的圆球，用长为L的细绳挂在光滑的墙壁上，当绳长L增大时，绳子的拉力T和墙壁的弹力N如何变化？

解：设想极端位置：L若变化为无穷大，

例1

则相当于绳直接挂着球，这时T=mg，N=0

∴ 当绳长增大时，T、N均减小。

（2）函数法：

用不变化的物理写出所求物理量随变化物理量（或是角度、长度等数学量）的函数表达式y=f(x)，从而看出物理量随变量如何变化。

例1中的不变量为球的重量G，设绳与竖直墙壁的夹角为θ（为变量），根据物理规律----共点力合力为零 则：可以得出函数式：

T=G/cosθ N=Gtgθ

当L增大时，θ变小 ， ∴cosθ-->大，tgθ-->小 ，而G不变

由此得出：T变小，N变小。

例2 在一块长木板上放一个质量为m的铁块，它们之间的摩擦系数为μ，木板放在水平地面上。若A端固定，缓慢地抬起木板的B端，问在木板的倾角θ增大的过程中，铁块受的摩擦力将如何变化？

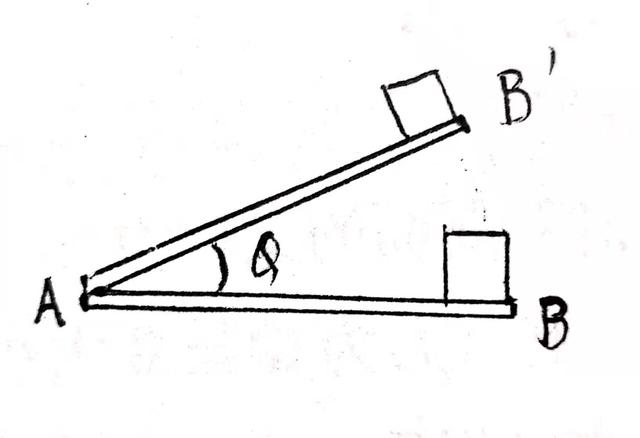
例2

分析：

开始θ角较小时，铁块受的是静摩擦力，木板缓慢转动可认为铁块为平衡状态，

则有ｆ1= mgsinθ

当θ角增大到某一数值时，铁块开始滑动， 受的是滑动摩擦力， 则有

ｆ2=μN=μmgcosθ

从以上的两种摩擦力的表达式上可看出ｆ1随θ的增大而增大，达到一最大值后，ｆ2又随θ的增大而减小，当θ为90°(即竖直时) 时，ｆ2为零。

此过程可画出下面函数图表示变化情况。

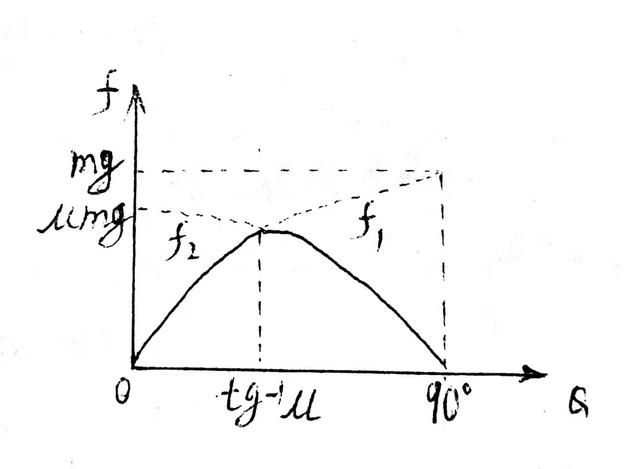
例2函数变化

（3）几何图形法

当物体处于三个共点力平衡时，三个共点力的大小、方向要符合平行四边形法则，当这个平行四边形的对角线（即合力）大小、方向不变时，用图形中的几何关系分析其它量变化的方法就是几何图形法。这种方法尤其是在函数式不易写出或分析遇到困难时，更显示出优越性。

例1 中的T、N的合力与G大小相等方向相反即为平行四边形的对角线不变，

当绳子变长时，N的方向也不变，可做出T’、N’的平行四边形对角线与原来一样，

从图形上可明显看出T’、N’比T、N短，

即 T’<T N’<N。

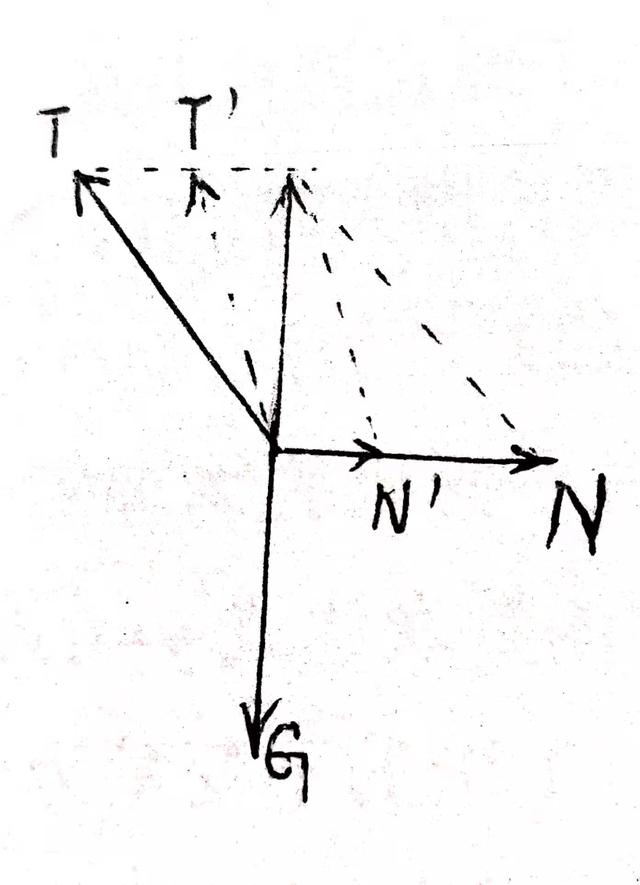
例1受力图

例3 光滑斜面与水平面的夹角是а，在斜面上放一个质量为m的圆球，再用光滑平板A挡住，现在缓慢地改变板A与斜面的夹角θ时，什么位置 A板对球的作用力最小？最小力为多少？

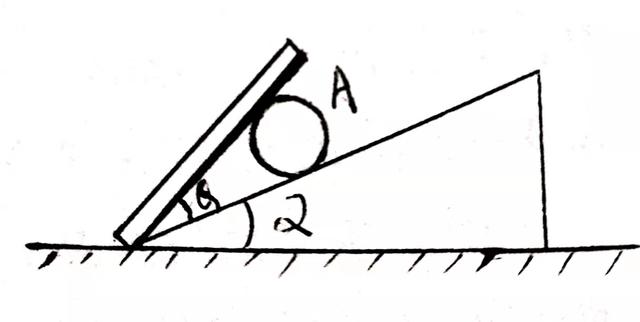
例3

分析：

如图 斜面的支持力N，板对球的作用力为T，其合力为G’与G大小方相等方向相反，

当θ角增大时，G’的大小方向都不变，且N的方向也不变（总是与斜面垂直）

变化的是T的大小和方向及N的大小，

但变化时仍应有T、N的合力为G’（大小方向都不变），可以做出几个虚线所示的平行四边形。

从分析图中可以看出：当T与N垂直时，线段最短，即这时T值最小，

可得θ=90°时 T=mgsina。

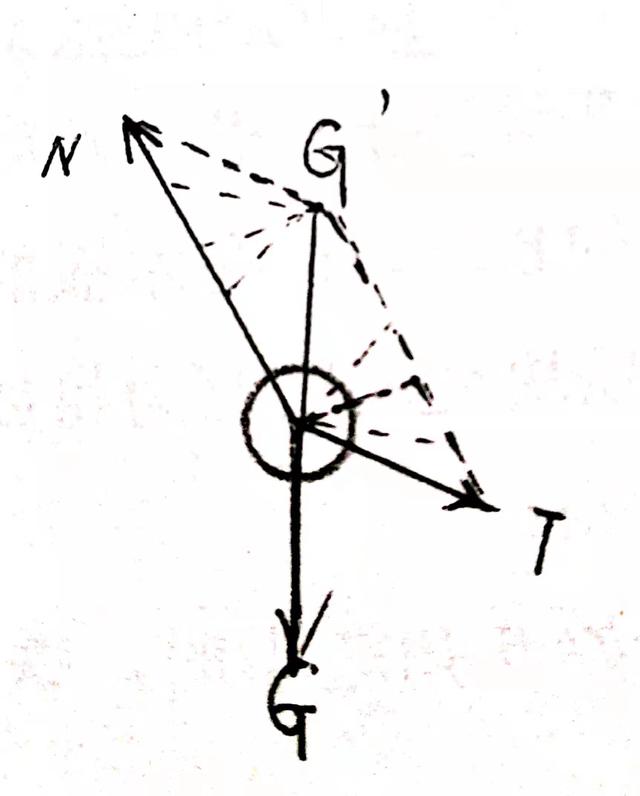
例3分析图