高中物理解题小技巧（2）——三力共点平衡特点的应用

三力共点平衡特点的应用

物体受共点力平衡的时候，一般条件是合力为零，合力距为零，推理得出的特殊规律：

物体受在同一平面内三个非平行力的作用，处于平衡状态时，具有以下两个规律：

（1）三个力矢量首尾相接，组成一个闭合三角形；

（2）三力作用线必交于一点。

应用此规律，在解决看似复杂的物体平衡问题中，通过物体的受力分析，找到受力的本质，运用以上规律，可以把复杂的平衡问题简单化。

例1、粗细均匀质量分布均匀的重为G的绳索，悬挂于同一水平面的A、B两点，若悬绳两端的切线与水平面的夹角均为θ，则悬点受到绳的拉力大小是多少？绳索中点处张力大小是多少？

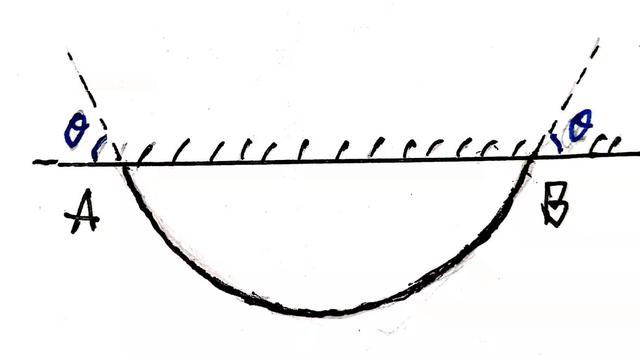
例1

解：分析绳索受力情况如图，只受三个力TA、TB、G。

绳索受这三力处于平衡状态，

所以：此三力为共点力，且合力为零，

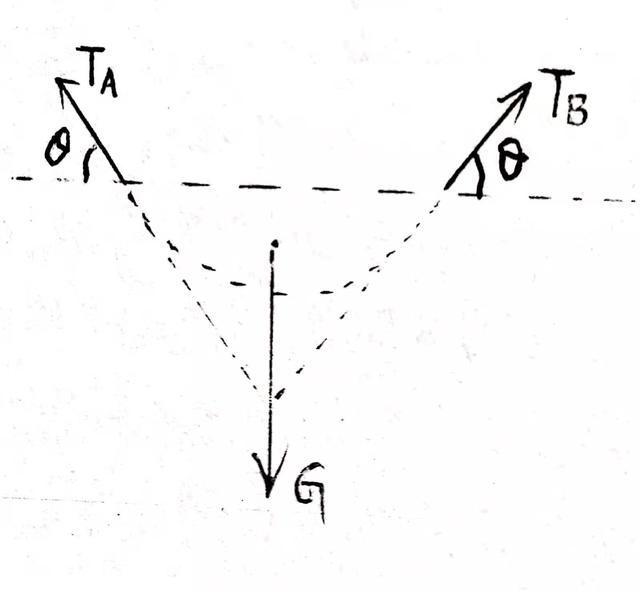
例1受力分析

有对称性可知，TA=TB

在竖直方向上力平衡，

∴ 2TAsinθ=G ∴ TA=G/（2sinθ）

悬点受到绳的拉力与TA是一对作用力和反作用力。

由牛顿第三定律可知大小也为G/（2sinθ）

绳索中点的张力大小为N= TAcosθ=G/（2 tgθ）

例2、一个质量为m=50千克的均匀圆柱体，放在台阶的旁边，台阶的高度h是柱体半径r的一半，如图（图为其截面），柱体与台阶触接处（图中P点）是粗糙的，现要在图中柱体的最上方A处施加一最小的力，使柱体刚能开始以P为轴向台阶上滚。

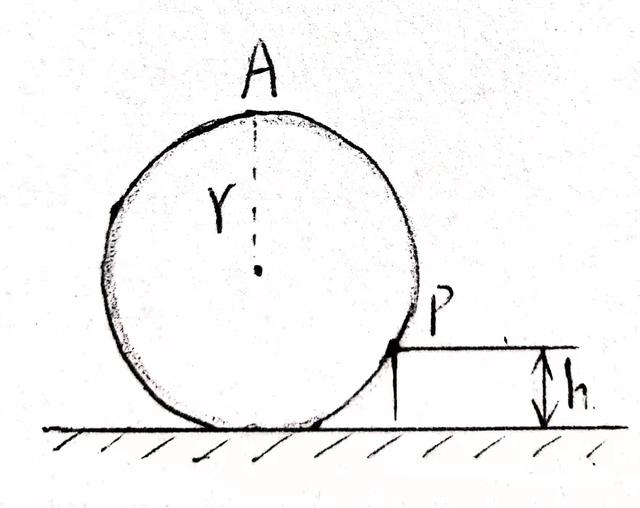
求：（1）所加的力的大小 （2）台阶对柱体的作用力的大小

解：（1）

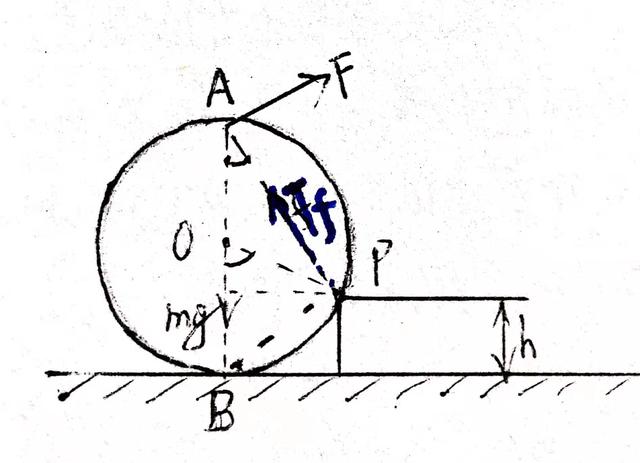
例2受力分析

以p点为转动轴，只有拉力F和重力G的力矩平衡，

此时地面对圆柱体的支持力N=0，

重力G的力矩是一定值，

若所加的力最小则F方向应垂直AP

（此时F的力臂最长，力最小）

由几何关系：r=2h

分析三角形各边长的比例，

得： ∠POB=600 ∴ ∠PAO=300

由物体受拉力F和重力G对p点轴力矩平衡

得 mg r sin600 = F2rcos300

得 F= mg/2＝ 250牛

（2）

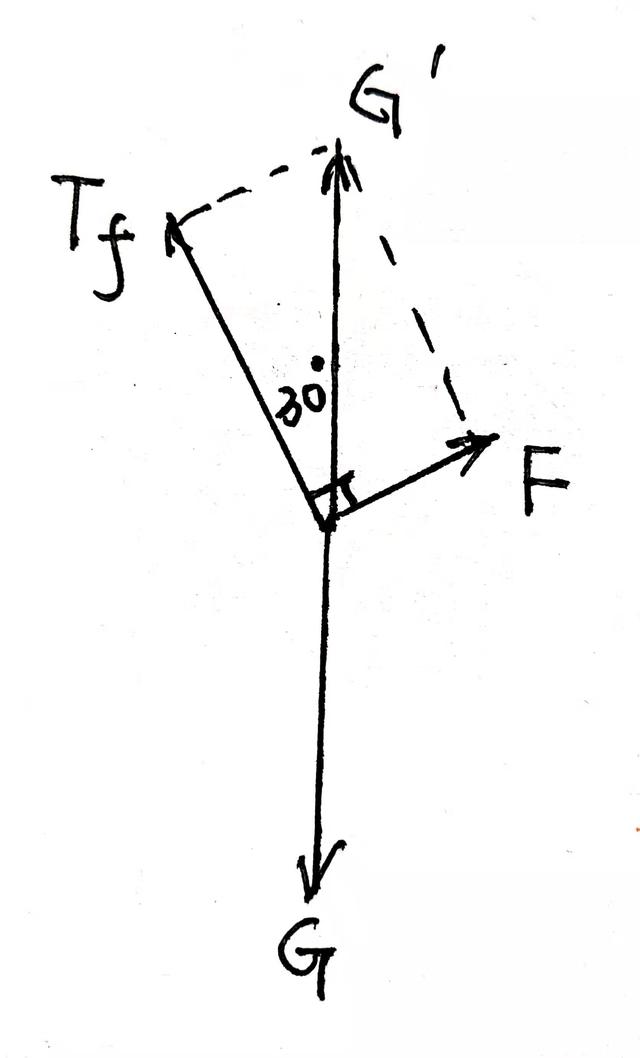
例2三力共点图

圆柱体p点所受的支持力和摩擦力的合力Tf.，即为台阶对圆柱体的作用力，

这时圆柱体所受三个力，F、G 、Tf必共点于A点，

圆柱体受三个力F、G、Tf、三力平衡 ∴必为共点力

由力的平衡，三角形关系，

可知：∴Tf =G cos300=432.5 牛

两道例题中都巧妙的应用了，物体受三力作用平衡，三力作用线必交于一点，三个力矢量首尾相接，组成一个闭合三角形的规律。

学习和应用物理规律，不仅仅是要记住一般的结论，一些在一般规律下得出来的特殊规律，在解决具体的问题中，能够熟练的应用，往往能起到事半功倍的作用。