2019年小学六年级毕业考试有这样一道题：

有一堆糖，奶糖占9/20，又加入16颗水果糖，奶糖占1/4，问原来有多少颗糖？

结果正确率只有28%，查看试卷发现，学生做法是：16÷（9/20-1/4)，这种错误占68%。这实际上是将糖果的总数看作单位“1”，没有搞清到底哪个是标准量（单位“1”），这是错误的根源。

为什么学生容易出现这种错误？

原因之一：学生没有真正学懂分数应用题，更多多的一直在模仿老师和教材。

现在六年级学生在做分数应用题时，老师一般都是要求学生依据模型，往里面套，比如已知单位“1”的量就是乘法，单位“1”的量未知就用除法。还有就是求单位“1”的量用，对应的量除以对应的分率等等。学生的错误就是这些死记硬背的恶果，只有部分真正做题认真，善于分析的学生才不会出错。

原因之二：这类问题平时练习较少，更多是做单位“1”的量不变这类题。学生形成惯性思维，做这类题根本不加思索，自认为信手拈来，太简单。

正确做法是什么？

标准解法：首先确定将奶糖颗数看作单位“1”，原因是奶糖的颗数一直没有发生变化。就要将原来水果糖的颗数和加入16颗后的颗数各占奶糖的几分之几表达出来？这是解题的核心步骤，即：原来水果糖是奶糖的11/9，加入16颗后，水果糖是奶糖的3/1，再配上线段图，让分析更加清晰，非常清楚看出3/1-11/9的差对应的就是加入的16颗水果糖的分率，所以正确做法是16÷（11/9-3/1)=9颗，9÷9/20=20颗，也就是说原来有20颗糖。

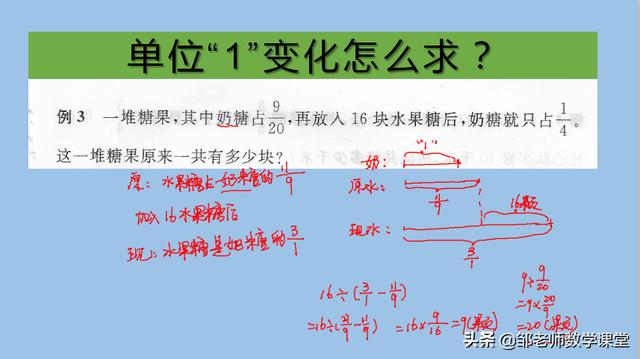
正确作法

此视频已经发布于头条号：小学数学免费课堂，此号专注小学数学经典题目的分享。

跟进训练:老师另外收集到3道相似题，请学生先自己做，再看相关解析过程。

3道相似训练题

三道同步精练解析：

1.抓住其余球数量不变，表达出原来红球占其余球的5/7，加入6个后，红球占其余球的1/1，那么6个球对应的分率就是1-5/7=2/7，6÷2/7=21个。一定要注意，21是其余球的个数，21÷（1-5/12）=36个才是原来总数。

2.原来女生占男生的7/5，加入15名女生后，女生占男生的3/2，所以15人对应是3/2-7/5=1/10，所以15÷1/10=150人，就是男生的人数。

3.此题的解法与上面两个题基本一致。