二次函数综合题：添加辅助线构造相似三角形和三角形中位线

已知抛物线C1：y=ax2+bx+3/2（a≠0）经过点A（﹣1，0）和B（3，0）．

（1）求抛物线C1的解析式，并写出其顶点C的坐标；

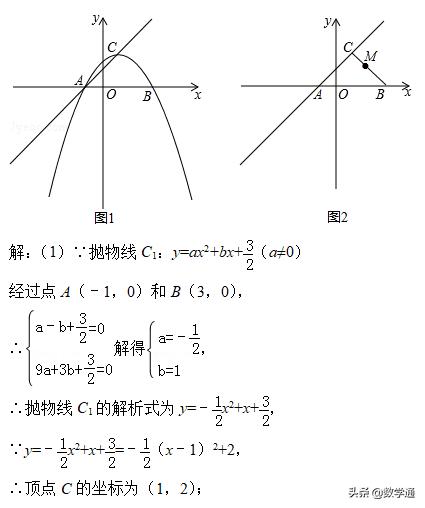
（2）如图1，把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2，此时点A，C分别平移到点D，E处．设点F在抛物线C1上且在x轴的下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标；

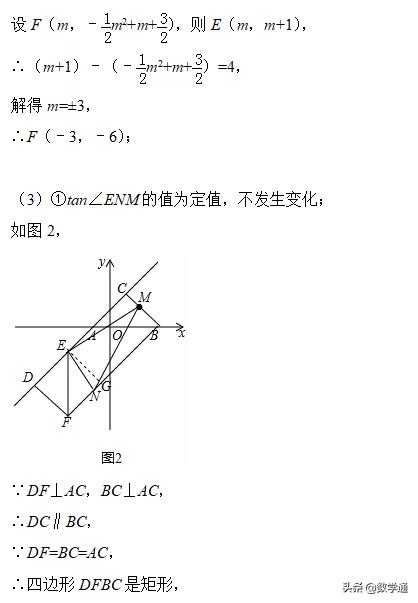
（3）如图2，在（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：

①tan∠ENM的值如何变化？请说明理由；

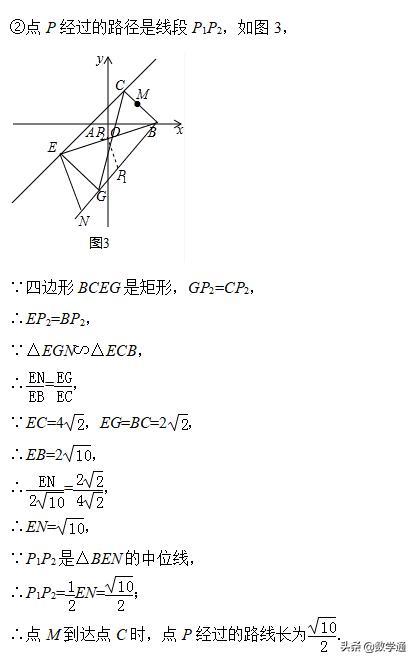
②点M到达点C时，直接写出点P经过的路线长．

考点分析：

二次函数综合题．

题干分析：

（1）根据待定系数法即可求得解析式，把解析式化成顶点式即可求得顶点坐标；

（2）根据A、C的坐标求得直线AC的解析式为y=x+1，根据题意求得EF=4，求得EF∥y轴，设F（m，﹣1/2m2+m+3/2），则E（m，m+1），从而得出（m+1）﹣（﹣1/2m2+m+3/2）=4，解方程即可求得F的坐标；

（3）①先求得四边形DFBC是矩形，作EG⊥AC，交BF于G，然后根据△EGN∽△EMC，对应边成比例即可求得tan∠ENM=EM/EN=2；

②根据勾股定理和三角形相似求得EN的值，然后根据三角形中位线定理即可求得．

解题反思：

本题是二次函数综合题，考查了待定系数法求二次函数的解析式，一次函数的解析式，等腰直角三角形的判定和性质，三角形相似的判定和性质，勾股定理的应用等，难点在于（3）作辅助线构造出相似三角形和三角形的中位线．