旋转与对称 探究并证明，北京中考第27题H8解读

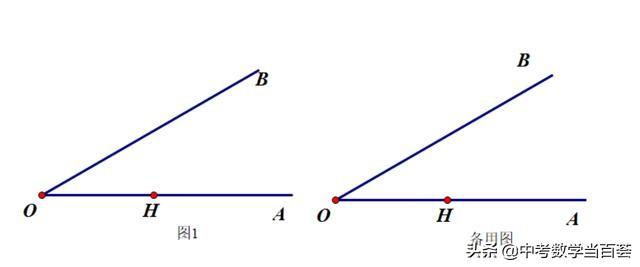
H8 已知∠AOB=30°，H为射线OA上一定点，OH=√3+1,P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN,连接ON.（1）依题意补全图1；（2）求证：∠OMP=∠OPN;（3）点M关于点H的对称点为Q，连接PQ.写出一个OP的值，使得对于任意点M总有ON=PQ，并证明.

分析

（1）依题意补图1

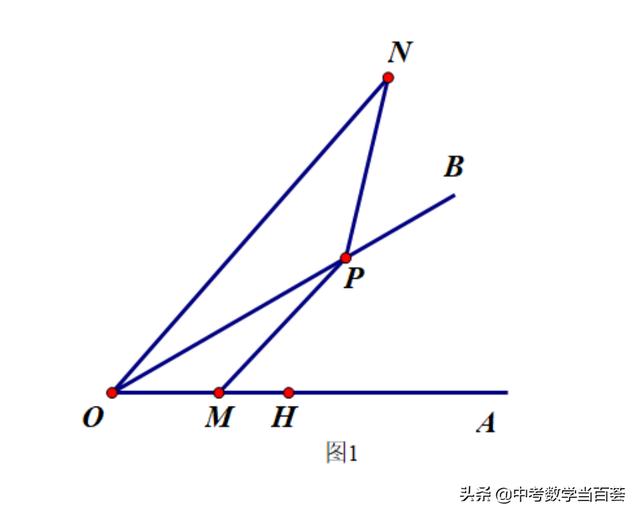
（2）如下图，延长MP至E，

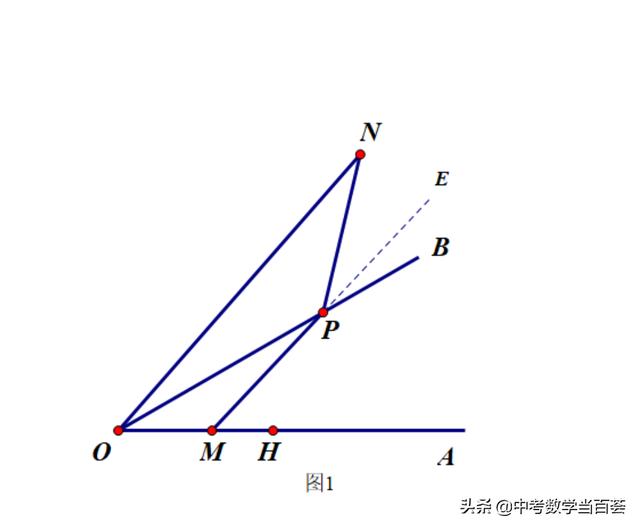
∵∠OPM=∠EPB，

且∠NPE=180°-∠MPN

=180°-150°=30°=∠POM

∴∠NPB=∠NPE+∠EPB

=∠POM+∠OPM=∠PMA

∴∠NPB=∠PMA

∴180°-∠NPB =180°-∠PMA

∴∠OMP=∠OPN

（3）如果OP=2，那么对于

任意点M总有ON=PQ

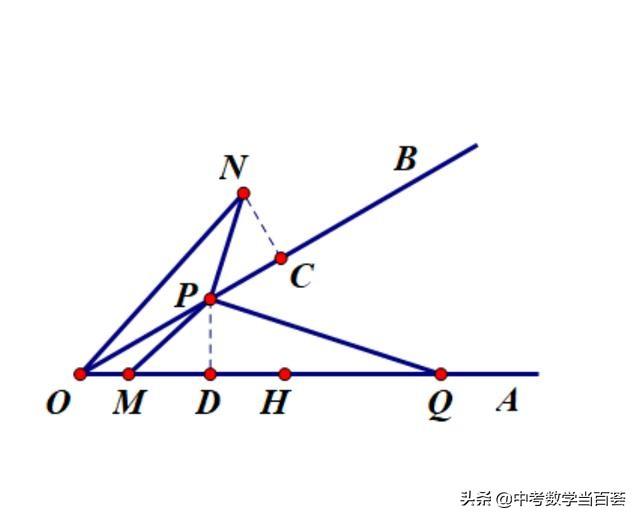
证明：作NC⊥OB,垂足为C，

作PD⊥OA,垂足为D，

在Rt△POD中，∠POD=30°,OP=2

∴PD=1,OD=√3,

∵OH=√3+1

∴DH=1

在Rt△PMD和Rt△PNC中，

由（2）知道∠PMD=∠PNC,

∠PDM=∠PCN=90°,PM=PN

∴Rt△PMD≌Rt△PNC

∴NC=PD=1,PC=MD

∵DQ=DH+HQ,DH=1,

HQ=HM=HD+MD=1+PC

∴DQ=DH+HQ=1+1+PC=2+PC

∵OC=OP+PC=2+PC

∴DQ=OC

在Rt△ONC和Rt△QPD中，

PD=NC,∠PDM=∠PCN=90°, DQ=OC

∴Rt△ONC≌Rt△QPD

∴ON=QP

综述

难点在第（3）问，构造直角三角形Rt△ONC和Rt△QPD，探究这两个直角三角形全等，

全等条件中，PD=NC,通过另外两个Rt△PMD和Rt△PNC

DQ=OC，较为繁琐，探究出OP=2，更是难点。