轻质物体时一种理想化模型，质量忽略不计，例如：“轻绳”，“轻杆”，“轻弹簧”等。

那么“轻质物体”所蕴含的信息有哪些呢？

一.轻质物体没有惯性

质量是惯性大小的唯一量度.因此速度可以发生突变,弹簧的弹力也可以发生突变.

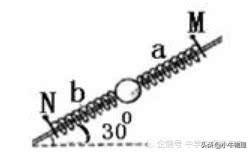
分析: 设小球的质量为m，沿杆斜上为正方向，刚开始受力平衡，则有：FN+FM-Gsin30°=0拔去销钉M瞬间，小球的加速度大小为6ｍ/ｓ２，方向可能向下，也可能向上。由牛顿第二定律得：FN-Gsin30°=±ma去销钉N瞬间，小球受M弹簧和重力G的作用，加速度为：a′==-11m/s2或1m/s2，故B，C正确.弹簧弹力发生突变.

例:某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力恒为 f．轻杆向右移动不超过l时，装置可安全工作．一质量为m的小车若以速度v撞击弹簧，将导致轻杆向右移动 l/4．轻杆与槽间的最大静擦力等于滑动摩擦力，且不计小车与地面的摩擦．

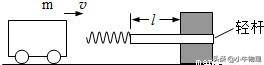
（1）若弹簧的劲度系数为k，求轻杆开始移动时，弹簧的压缩量x；

（2）求为使装置安全工作，允许该小车撞击的最大速度vm；

（3）讨论在装置安全工作时，该小车弹回速度v′和撞击速度v的关系．

二.轻质物体在任何状态下合力为零

轻质物体在任何状态下合力为零,但并不意味着轻质物体只能处于平衡状态.

例:如图所示，长为l的轻绳，一端用轻环套在水平光滑的横杆上，另一端连接一质量为m的小球.开始时，将系球的绳子绷紧并转到与横杆平行位置，然后轻轻放手，当绳子与横杆成θ角时，小球速度在水平方向和竖直方向上的分量大小分别是多少？

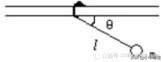
分析:因为绳和环套都是轻质,满足合力为零,故小球做自由落体运动.轻环套与小球在水平方向不受外力，速度方向不发生改变，小球速度在水平方向的分量大小为：0；(2glsinθ)的平方根

三.轻质物体起着传递能量作用

对于本身形变不明显的"轻绳轻杆"由于没有质量,故无法承载机械能,因此在许多做功和能量问题时,往往是起着"传递"能量的中间角色.

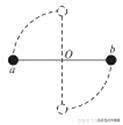
例:如图所示,在两个质量分别为m和2m的小球a和b之间,用一根长为L的轻杆连接,两小球可绕穿过轻杆中心O的水平轴无摩擦转动。现让轻杆处于水平位置后无初速释放,重球b向下、轻球a向上产生转动,在杆转至竖直的过程中( )

A．b球的重力势能减少,动能增加

B．a球的重力势能增加,动能减少

C．a球和b球的总机械能守恒

D．轻杆对a球做正功，对b球做负功，并且对两球做功的绝对值相等

通过轻杆分别对两球做功的方式实现能量的转移.