「高中数学」证明：圆的内接三角形中，正三角形的面积最大

圆的最大内接三角形的求解，除了用到正弦定理的变形以及圆的几何性质，还用到了均值不等式的变形、凸函数的概念等。

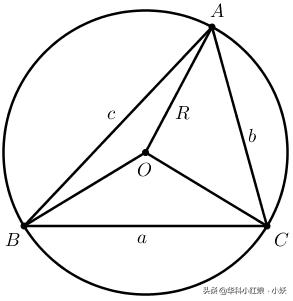
圆的内接三角形

首先将三角形ABC的面积表示出来：

这里用到了正弦定理的变形。

如下图，做辅助线。

做如图辅助线

在三角形OBP中，可得：

同理可得：

三角形ABC的面积可化简为

这一步用到了均值不等式的变形。

又因为正弦函数为定义域R上的凸函数，可得：

所以

当且仅当A=B=C时不等式取等号。

即

如此，可以证明，圆的内接三角形中，正三角形的面积最大。

如需要进一步求出该三角形的边长或者高，也是很简单的啦。

看似很简单的一道证明题，实际上却用到了高中数学的诸多知识点；在实际的解题中，如果是选择或者填空题，我们就可以直接运用这个结论啦！