经典再现20——等边三角形中的不等式

题：如图1，等边ΔABC的边长为1，D、E分别是AB，AC上的点，且AD=CE.

求证：DE≥1/2.

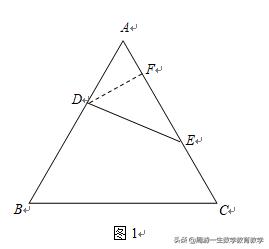
思路1：欲证DE≥1/2，就是求DE的最小值为1/2.因为DE的长决定于AD的长，因此，以AD为自变量建立DE与AD的函数关系式.

证法1：设AD=x，DE=y，则AE=1-CE=1-x.

作DF⊥AE于F.

因为∠A=60°，

所以AF=AD/2=x/2，DF =√3x/2，

所以EF=1-x-x/2=1-3x/2,

所以y=√(DF^2+EF^2)

=√[(√3x/2)^2+(1-3x/2)^2]

=√(3x^2/4+1-3x+9x^2/4)

=√(3x^2-3x+1)

=√[3(x-1/2)^2+1/4]

所以，当x=1/2时，

y最小值=√(1/4)=1/2，

所以DE≥1/2.

思路2：欲证DE≥1/2，只需证明2DE≥BC.将DE沿AC平移，使点E与点C重合，让DE与BC在同一三角形中以便比较大小.

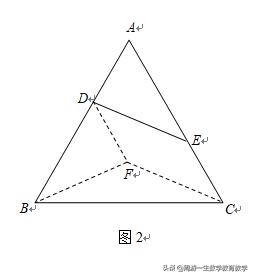
证法2：将DE沿AC平移到CF（如图2），连接DF，BF.则

CF=DE，四边形DECF是平行四边形，

所以CE=DF，

因为ΔABC使等边三角形，AD=CE，

所以AD=DF，AE=BD，

又∠A=∠BDF，

所以ΔADE≌ΔDFB，

所以BF=DE，

因为BF+CF≥BC（当点D为AB中点时，DE为ΔABC的中位线，F为BC中点，等号成立），

所以2DE≥BC，

所以DE≥BC/2，

即DE≥1/2.