初中数学几何最值问题不用愁，掌握套路算的快（二）

上一篇文章中讲解了最值问题的前两种类型，接下来，我们讲一下后三个。

三、两条线段之和的最小值，通常以两定点，一动点的方式出现，也叫将军饮马模型。

将军饮马

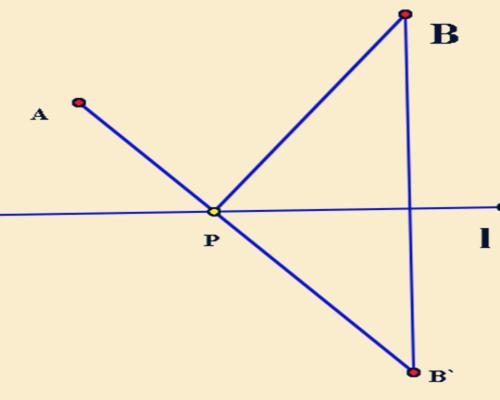
将军饮马模型指的是两个定点A，B，一个动点P在直线上，求PA+PB的最小值。通过做对称点，运用垂直平分线的性质，这个问题就可以解决。接下来，看一下它在题中出现的方式。

将军饮马

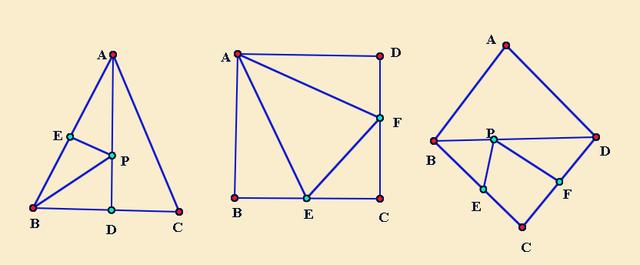
左图，三角形是一个等腰三角形，AD是高，E是AB的中点，求PE+PB的最小值。这里两个点E和B，一个运点P，做B的对称点就是C，实际上是求CE的长度。

中图，正方形，E是中点，F是CD上一动点，求AE+AF的最小值。两个定点A和E，一个动点F，作E点的称点E'，即可解决。

右图，菱形，E,F分别是中点，P是BD上一动点，符合两定一动，作对称点即可解决。

将军饮马模型在考试中应用比较常见，也比较简单，同学位要认真学习一下。

四、三条线段之和的最小值

三条线段之和主要有两个模型。

平移加将军饮马

1、平移加将军饮马。

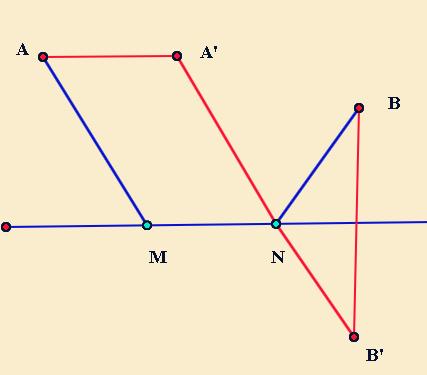
在这个模型中，有两定点，两动点，但两动点的距离一样，把两动点组成的线段看成一个点，就是将军饮马。如图所示，A，B两个动点，M，N两点在直线上移动，MN一定，求AN+MN+NB的最小值。只需比将军饮马多作一个A点的平移即可。的

四边形周长

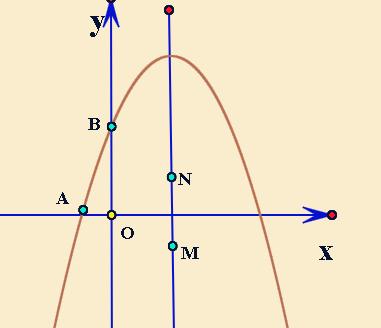
例题：抛物线与坐标轴交于A，B。 M，N是对称轴上的两点，MN=a，求四边形AMNB的周长。像这一类型，你会做吗？看起来很复杂，只要按照步骤做就可以了。

2、两次运用将写饮马

三周形周长

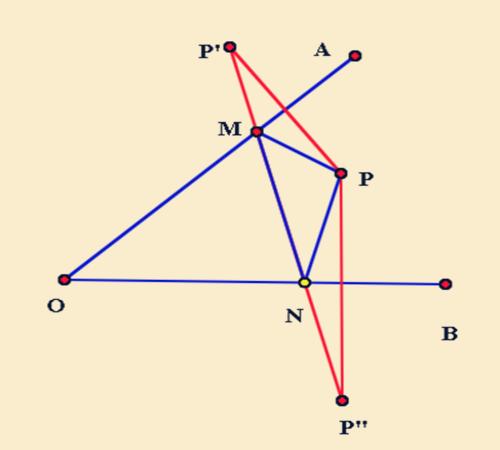
一定点，两动点，两个动点在两条直线上。如图，P是动点，M，N分别是OA，OB上的动点，求PM+MN+PN的最小值。就是分别作定点P的对称点，相连即可解决。

例题：上图中，角AOB=45，OP=10，求PM+MN+PN的最小值。给出45度的角，是为了可能构建一个等腰直角三角形OP'P''方便我们计算。当然也可以是30度，可以构造出一个等边三角形。

五、两线段之差的绝对值的最大值

两线段之差

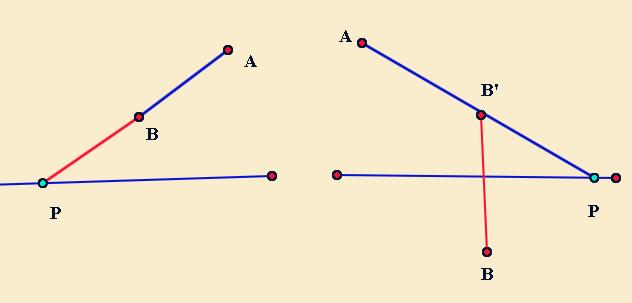
两定点，一动点，动点在一条直线上。基本分为两种情况。左图是两定点在直线的同侧，直接延长AB交直线于P，P就是所求的点。右图是两定点在直线的两侧，需要做一定点的对称点，延长后交直线的点P就是所求的点。

两线段之差较多与抛物线相结合，同学位可以了解一下。