中点模型
【模型1】倍长
1、倍长中线;2、倍长类中线;3、中点遇平行线延长相交
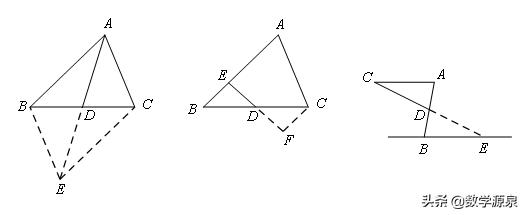
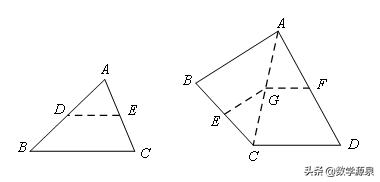
【模型2】遇多个中点,构造中位线
1、直接连接中点;2、连对角线取中点再相连
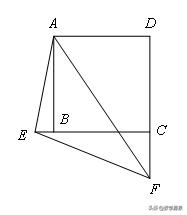
【例1】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.
(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;
(2)如图2,当点F在AB的延长线上时,线段GE、GC有怎样的数量和位置关系,写出你的猜想,并给予证明;
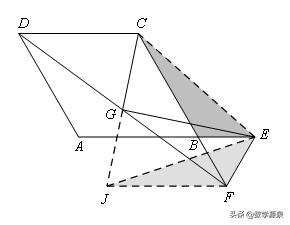
(3)如图3,当点F在CB的延长线上时,(2)问中的关系还成立吗?写出你的猜想,并给予证明.
【解答】
(1)延长EG交CD于点H
易证明△CHG≌△CEG,则GE=3√3
(2)延长CG交AB于点I,
易证明△BCE≌△FIE,则△CEI是等边三角形,GE=√3GC,且GE⊥GC
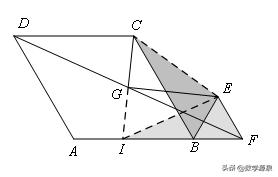
(3)
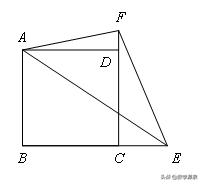
【例2】如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
(1)求证:CE=CF;
(2)若∠ABC=120°,点G是线段AF的中点,连接DG、EG,求证:DG⊥EG.
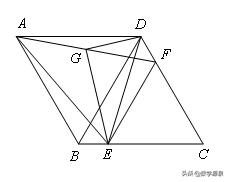
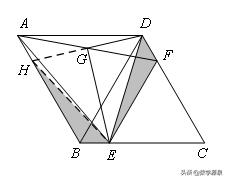
【解答】
(1)证明△ABE≌△ADF即可;
(2)延长DG与AB相交于点H,连接HE,证明△HBE≌△EFD即可
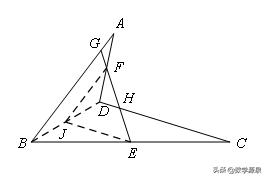
【例3】如图,在凹四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA交EF延长线于G点,CD交EF于H点,求证:∠BGE=∠CHE.
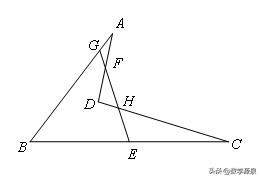
【解答】
取BD中点可证,如图所示:
角平分线模型
【模型1】构造轴对称
【模型2】角平分线遇平行构等腰三角形
【例4】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交边CD于F点,交AD边于H,延长BA到G点,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为_______.
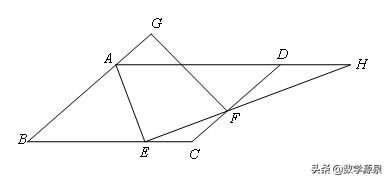
【解答】
延长FE、AB交于点I,易得CE=CF,BA=BE,设CE=x,则BA=CD=3+x,BE=7-x,
3+x=7-x,x=2,AB=BE=5,AE=,作AJ⊥BC,连接AC,求得GF=AC=3
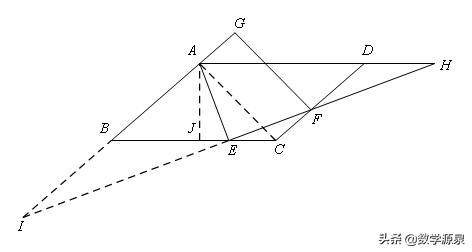
手拉手模型
【条件】OA=OB,OC=OD,∠AOB=∠COD
【结论】△OAC≌△OBD,∠AEB=∠AOB=∠COD(即都是旋转角);OE平分∠AED
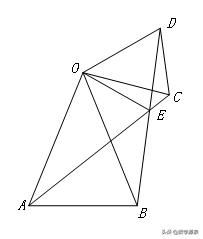
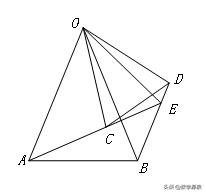
【例5】(2014重庆市A卷)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为________.
【答案】6√5/5
【例6】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE,AG⊥BE于F,交BC于点G,求∠DFG.
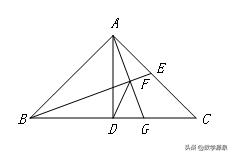
【答案】45°
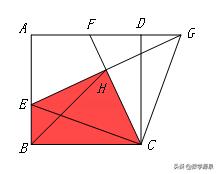
【例7】(2014重庆B卷)如图,在边长为6√2的正方形ABCD中,E是AB边上一点,G是AD延长线一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE、BH.若BH=8,则FG=_____________.
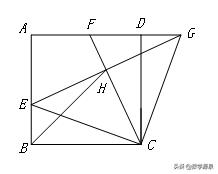
【答案】5√2
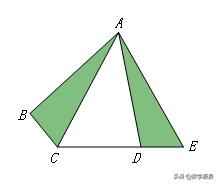
邻边相等对角互补模型
【模型1】
【条件】如图,四边形ABCD中,AB=AD,∠BAD+∠BCD=∠ABC+∠ADC=180°
【结论】AC平分∠BCD
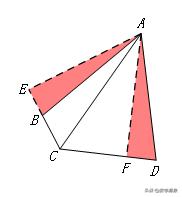
【模型2】
【条件】如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°
【结论】① ∠ACB=∠ACD=45°; ② BC+CD=√2AC
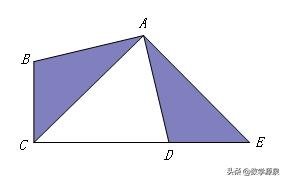
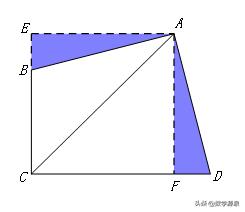
【例8】如图,矩形ABCD中,AB=6,AD=5,G为CD中点,DE=DG,FG⊥BE于F,则DF为_____.
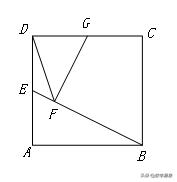
【答案】9√5/5
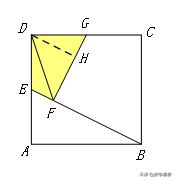
【例9】如图,正方形ABCD的边长为3,延长CB至点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连结ON,则ON的长为__________.
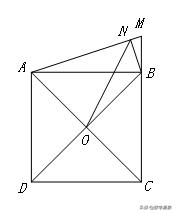
【答案】6√5/5
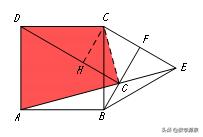
【例10】如图,正方形ABCD的面积为64,△BCE是等边三角形,F是CE的中点,AE、BF交于点G,则DG的长为___________.
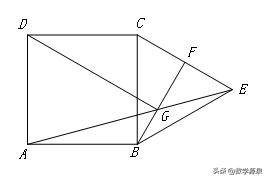
【答案】4√3+4
半角模型
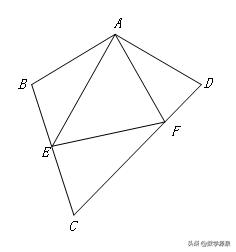
【模型1】
【条件】如图,四边形ABCD中,AB=AD,∠BAD+∠BCD=∠ABC+∠ADC=180°,∠EAF=
1/2∠BAD, 点E在直线BC上,点F在直线CD上【结论】BE、DF、EF满足截长补短关系
【模型2】
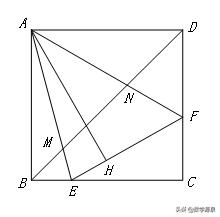
【条件】如图,在正方形ABCD中,已知E、F分别是边BC、CD上的点,且满足∠EAF=45°,AE、AF分别与对角线BD交于点M、N.
【结论】①BE+DF=EF;
②
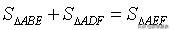
;③AH=AB;
④
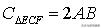
;⑤BM2+DN2=MN2;
⑥△ANM∽△DNF∽△BEM∽△AEF∽△BNA∽△DAM(由AO:AH=AO:AB=1:√2可得到△ANM和△AEF相似比为1:√2)
⑦
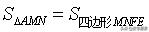
⑧△AOM∽△ADF;△AON∽△ABE;
⑨△AEN为等腰直角三角形,∠AEN=45°,△AFM为等腰直角三角形,∠AFM=45°;⑩A、M、F、D四点共圆,A、B、E、N四点共圆,M、N、F、C、E五点共圆.
【模型2变形】
【条件】在正方形ABCD中,已知E、F分别是CB、DC延长线上的点,且满足∠EAF=45°
【结论】BE+EF=DF
【模型2变形】
【条件】在正方形ABCD中,已知E、F分别是BC、CD延长线上的点,且满足∠EAF=45°
【结论】DF+EF=BE
【例11】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=__________.
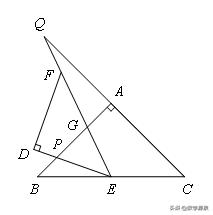
【解答】连接AE,题目中有一线三等角模型和半角模型
设AC=x,由△BPC∽△CEQ得
BP/CE=BE/CQ, 3/((√2/2)x)=(√2/2)x/(x+12),解得x=12
设PG=y,由AG2+BP2=PG2得32+(12-3-x)2=x2,解得x=5
【例12】如图,在菱形ABCD中,AB=BD,点E、F在AB、AD上,且AE=DF.连接BF与DE交于点G,连接CG与BD交于点H,若CG=1,则S四边形BCDQ=__________.
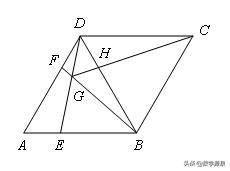
【解答】√3/4
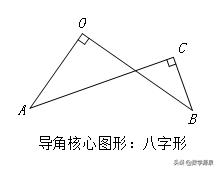
一线三等角模型
【条件】∠EDF=∠B=∠C,且DE=DF
【结论】△BDE≌△CFD
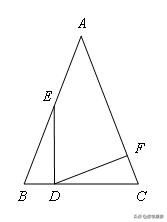
【例13】如图,正方形ABCD中,点E、F、G分别为AB、BC、CD边上的点,EB=3,GC=4,连接EF、FG、GE恰好构成一个等边三角形,则正方形的边为__________.
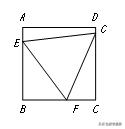
【解答】如图,构造一线三等角模型,△EFH≌△FGI
则BC=BF+CF=HF-BH+FI-CI=GI-BH+HE-CI=7√3/3
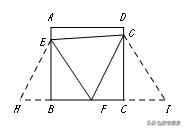
弦图模型
【条件】正方形内或外互相垂直的四条线段
【结论】新构成了同心的正方形
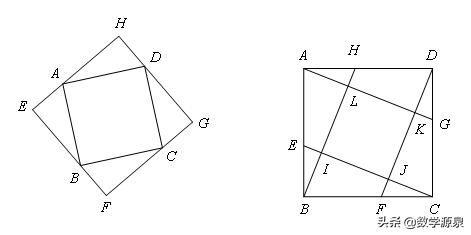
【例14】如图,点E为正方形ABCD边AB上一点,点F在DE的延长线上,AF=AB,AC与FD交于点G,∠FAB的平分线交FG于点H,过点D作HA的垂线交HA的延长线于点I.若AH=3AI,FH=2√2,则DG=__________.
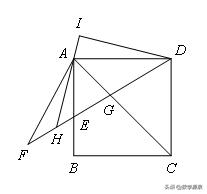
【解答】17√2/4
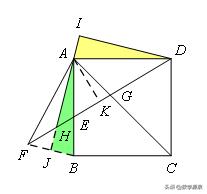
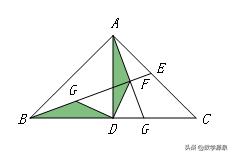
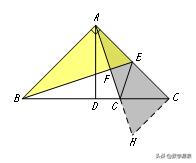
【例15】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是AC中点,连接BE,作AG⊥BE于F,交BC于点G,连接EG,求证:AG+EG=BE.
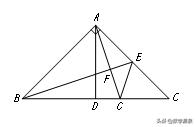
【解答】过点C作CH⊥AC交AG的延长线于点H,易证
最短路径模型
【两点之间线段最短】
1、将军饮马
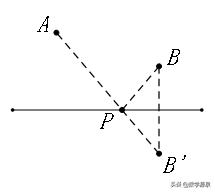
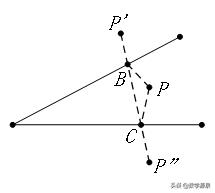
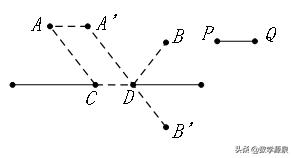
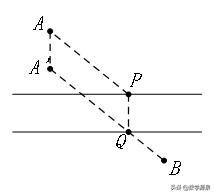
2、费马点
【垂线段最短】
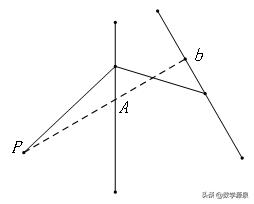
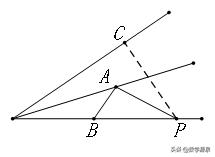
【两边之差小于第三边】
【例16】如图,矩形ABCD是一个长为1000米,宽为600米的货场,A、D是入口,现拟在货场内建一个收费站P,在铁路线BC段上建一个发货站台H,设铺设公路AP、DP以及PH之长度和为l,求l的最小值.
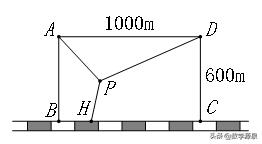
【解答】600+500√3,点线为最短.
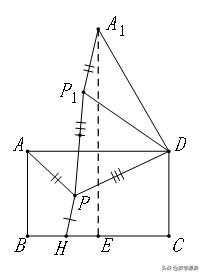
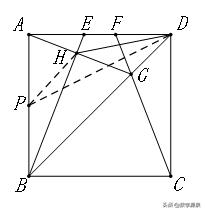
【例17】如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于H,若正方形的边长为2,则线段DH长度的最小值为______________________.
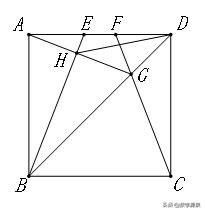
【解答】如图,取AB中点P,连接PH、PD,易证PH≥PD-PH即DH≥√5-1.
课后练习题
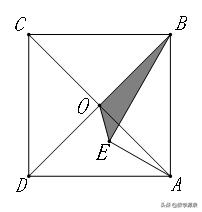
【练习1】如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90°,AC、BD交于O.已知AE、BE的长分别为3、5,求三角形OBE的面积.
【解答】5/2
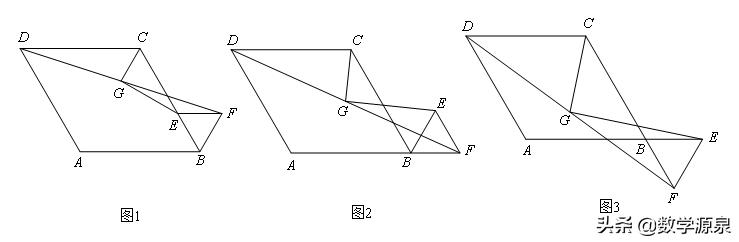
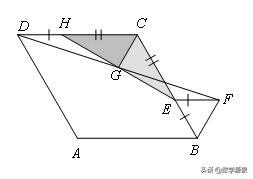
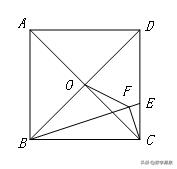
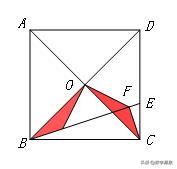
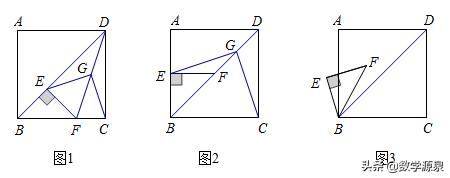
【练习2】已知:如图1,正方形ABCD中,为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
求证:EG=CG且EG⊥CG;
将图1中△BEF绕B逆时针旋转45°,如图2所示,取DF中点G,连接EG,CG,问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?
【解答】
略
方法一:如图所示
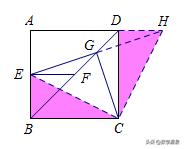
方法二:如图所示
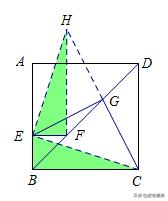
(3)
方法一:
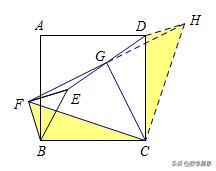
方法二:
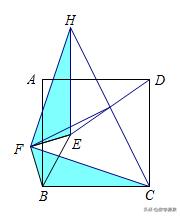

 加载中,请稍侯......
加载中,请稍侯......
精彩评论