中考冲刺，构建函数模型灵活求解实际问题

日常生活中普遍存在的成本最低、利润最高、产量最大、效益最好、用料最省等实际问题，用函数知识对信息的进行加 工与分析，建立相应的函数关系，确定变量的限制条件，运用函数方法进行求解，最后再解决实际问题。

而求解问题关键涉及到数学建模思想应用。数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化建立能近似刻画并"解决"实际问题的一种强有力的数学手段,将方程问题、不等式问题利用函数模型来解决,有时会收到意想不到的效果.下面谈谈通过建立函数模型求解问题。

1. 某校厨房有一太阳能热水器，其水箱的最大蓄水量为1200升．已知水箱的蓄水量y（升）与匀速注水时间x（分钟），在没有放水的情况下有如下关系：

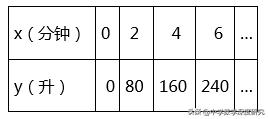
（1） 根据上表中的数据，在上图的坐标系中描出相应的各点，顺次连接各点后，你发现这些点在哪一种图形上猜一猜，符合这个图形的函数解析式；

（2）请验证上表各点的坐标是否满足函数解析式，归纳你的结论，并写出自变量x的取值范围．

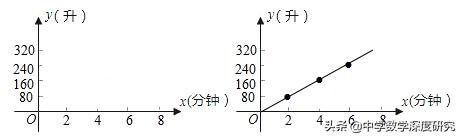
解：（1）描点连接如右图，发现四个点在经过原点的一条直线上，可以猜想为y=kx（k≠0）；（2）将x=2，y=80代入y=kx（k≠0）中，得k=40，那么y=40x． 验证：把x=4，y=160代入所得的函数式中，左边=160，右边=40×4=160；因此左边=右边，即点（4，160）满足该函数式，同理可验证（6，240）也满足该函数式，因此符合要求的函数解析式是y=40x，x的取值范围是0≤x≤30．

2（2019•上城区一模）小华有一个容量为8GB（1GB＝1024MB）的U盘，U盘中已经存储了1个视频文件，其余空间都用来存储照片．若每张照片占用的内存容量均相同，照片数量x（张）和剩余可用空间y（MB）的部分关系如表：

（1）求出y与x之间的关系式．

（2）求出U盘中视频文件的占用内存容量．

（3）若U盘中已经存入1000张照片，那么最多还能存入多少张照片？

【解析】（1）设y与x之间的关系式为y＝kx+b，根据题意得，

200k+b=5400, 100k+b=5700，解得k=-3, b=6000，

故y与x之间的关系式为y＝﹣3x+6000；

（2）根据题意可知U盘中视频文件的占用内存容量为1024×8﹣6000＝2192（MB）；

（3）当x＝1000时，y＝﹣3×1000+6000＝3000，

故最多还能存入3000张照片．

3．（2019•蜀山区一模）小明大学毕业后积极响应政府号召回乡创业，准备经营水果生意，他在批发市场了解到某种水果的批发单价与批发量有如下关系

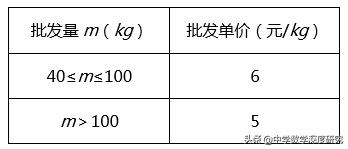
（1）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；并在如图的坐标系网格中画出该函数图象；指出资金金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．

（2）经市场调查，销售该种水果的日最高销量n（kg）与零售价x（元/kg）之间满足函数关系n＝440﹣40x，小明同学拟每日售出100kg以上该种水果（不考虑损耗），且当日零售价不变，请问他批发多少千克该种水果，零售价定为多少元时，能使当日获得的利润最大，最大利润是多少？

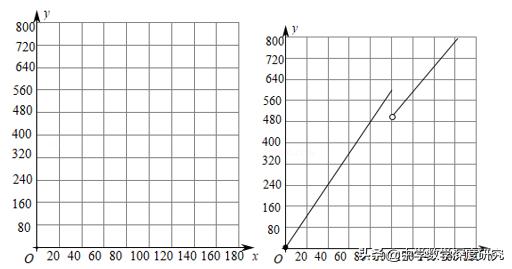
【分析】（1）取点（0，0）和（40，240）连线即可得40≤m≤100时的图象；取点（100，500）和（120，600）即可得m＞100时的图象；

（2）利用利润等于销售量乘以每千克的零售价减去批发价，化简为关于x的二次函数即可求解．

【解答】（1）由图象可知，当资金金额500＜w≤600时，以同样的资金可以批发到较多数量的该种水果．

（2）∵销售该种水果的日最高销量n（kg）与零售价x（元/kg）之间满足函数关系n＝440﹣40x，

∵小明同学拟每日售出100kg以上该种水果，则其批发单价为5元/kg，设利润为L元，则由题意得：

L＝n（x﹣5）＝（440﹣40x）×（x﹣5）＝﹣40x²+640x﹣2200＝﹣40（x﹣8)²+360

∴当x＝8，n＝440﹣40×8＝120时，时，能使当日获得的利润最大，最大利润为360元．

答：他批发120千克该种水果，零售价定为8元时，能使当日获得的利润最大，最大利润是360元

4．（2019春•南岸区校级月考）某学校为了控制冬季传染病的传播，对各教室进行消毒．为了得到时间t（单位：m）与教室里空气中药物含量y（单位：mL/m3）之间的关系，测得以下数据：

（1）根据上表，请在以时间t为横坐标，空气中药物含量y为纵坐标建立的直角坐标系内描出上述各点，并用平滑曲线把这些点一次连接；

（2）请根据直角坐标系内各点的变化趋势，确定y与t的函数模型以及函数表达式．

（3）根据药物性质可知，当教室空气中含量小于3mL/m3大于1/2mL/m3时，消毒效果最好．最好的消毒效果时间能持续多久？

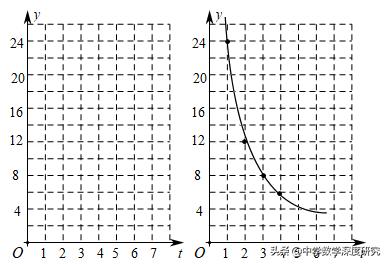
【解析】（1）如图所示：

（2）设y与t的函数解析式为：y＝k/t，且过点（1，24）

∴k＝1×24＝24,∴y与t的函数解析式为：y＝24/t

（3）当y＝3时，t＝8，当y＝1/2时，t＝48.

∴最好的消毒效果持续时间＝48﹣8＝40（小时）

答：最好的消毒效果时间持续40小时．

5．（2019•厦门一模）某村启动"脱贫攻坚"项目，根据当地的地理条件，要在一座高为1000m的山上种植一种经济作物．农业技术人员在种植前进行了主要相关因素的调查统计，结果如下：

①这座山的山脚下温度约为22°C，山高h（单位：m）每增加100m，温度T（单位：°C）下降约0.5°C；

②该作物的种植成活率p受温度T影响，且在19°C时达到最大．大致如表一：

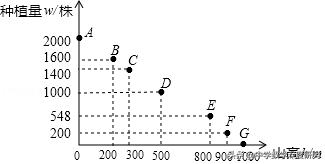
③该作物在这座山上的种植量w受山高h影响，大致如图：

（1）求T关于h的函数解析式，并求T的最小值；

（2）若要求该作物种植成活率p不低于92%，根据上述统计结果，山高h为多少米时该作物的成活量最大？请说明理由．

【分析】（1）根据"这座山的山脚下温度约为22°C，山高h（单位：m）每增加100m，温度T（单位：°C）下降约0.5°C"，可以得出T关于h的函数解析式，根据T随h的增大而减小求T的最小值；

（2）成活率p与温度T之间的关系大致符合一次函数关系，先求出一次函数关系式；由图知，除点E外，其余点大致在一条直线上，然后求出一次函数关系式，最后求出成活量与h的函数关系式，从而确定山高h为300米时该作物的成活量最大．

练习：

1．（2019•临海市一模）如图1，皮皮小朋友燃放一种手持烟花，这种烟花每隔l.4秒发射一发花弹，每一发花弹的飞行路径，爆炸时的高度均相同．皮皮小朋友发射出的第一发花弹的飞行高度h（米）随飞行时间t（秒）变化的规律如下表．

（1）根据这些数据在图2的坐标系中画出相应的点，选择适当的函数表示h与t之间的关系，并求出相应的函数解析式；

总结：建立两个变量之间的函数模型的具体步骤如下:

(1)将实验得到的数据在直角坐标系中描出;(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;(3)进行检验;(4)应用这个函数模型解决问题.