知识要点：

一元二次函数的区间最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论。一般分为：对称轴在区间的左边，中间，右边三种情况.

二、例题分析归类：

（一）、正向型

是指已知二次函数和定义域区间，求其最值。对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。此类问题包括以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1. 轴定区间定

二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是“定二次函数在定区间上的最值”。

2、轴定区间变

二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是“定函数在动区间上的最值”。

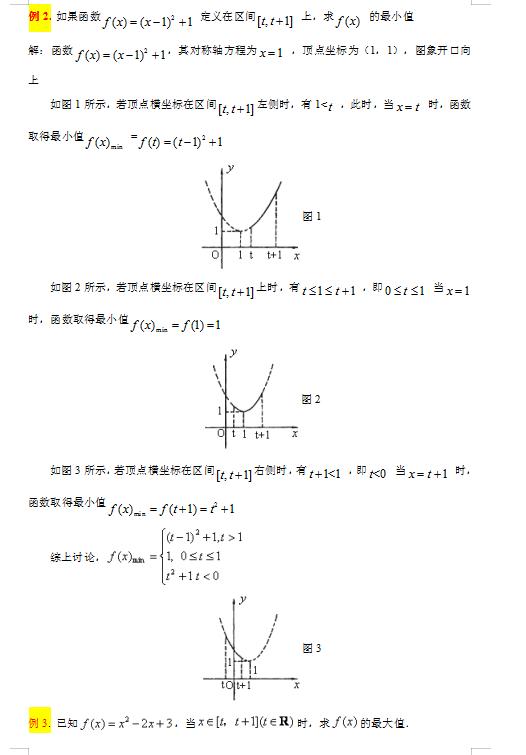
观察前两题的解法，为什么最值有时候分两种情况讨论，而有时候又分三种情况讨论呢？这些问题其实仔细思考就很容易解决。不难观察：二次函数在闭区间上的的最值总是在闭区间的端点或二次函数的顶点取到。第一个例题中，这个二次函数是开口向上的，在闭区间上，它的最小值在区间的两个端点或二次函数的顶点都有可能取到，有三种可能，所以分三种情况讨论；而它的最大值不可能是二次函数的顶点，只可能是闭区间的两个端点，哪个端点距离对称轴远就在哪个端点取到，当然也就根据区间中点与左右端点的远近分两种情况讨论。根据这个理解，不难解释第二个例题为什么这样讨论。

对二次函数的区间最值结合函数图象总结如下：

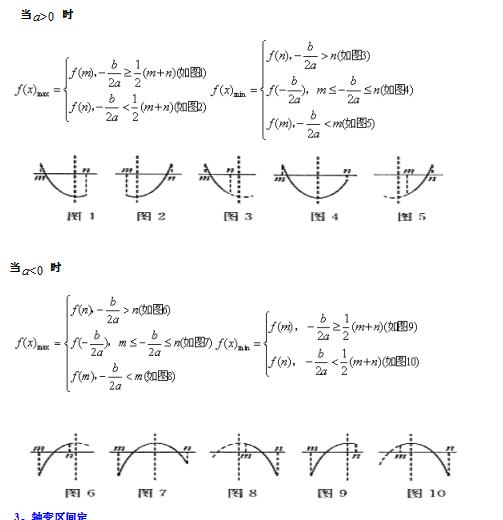
3、轴变区间定

二次函数随着参数的变化而变化，即其图象是运动的，但定义域区间是固定的，我们称这种情况是“动二次函数在定区间上的最值”。

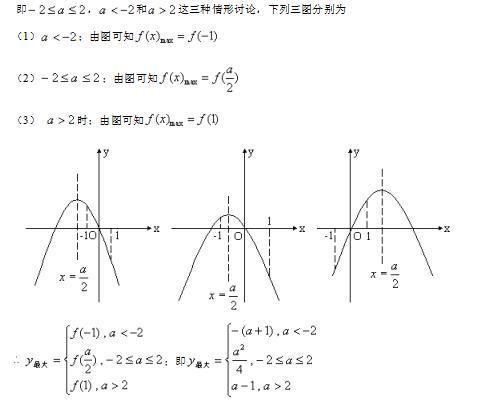
4. 轴变区间变

二次函数是含参数的函数，而定义域区间也是变化的，我们称这种情况是“动二次函数

在动区间上的最值”。

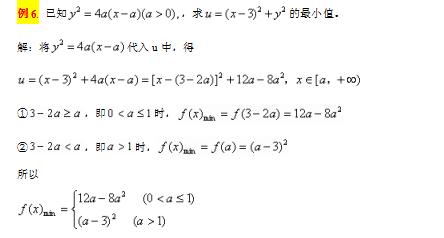
（二）、逆向型

是指已知二次函数在某区间上的最值，求函数或区间中参数的取值。

解后反思：若函数图象的开口方向、对称轴均不确定，且动区间所含参数与确定函数的参数一致，可采用先斩后奏的方法，利用二次函数在闭区间上的最值只可能在区间端点、顶点处取得，不妨令之为最值，验证参数的资格，进行取舍，从而避开繁难的分类讨论，使解题过程简洁、明了。

三、巩固训练