中考数学一次函数

2019年全国各地中考题中，罕见用一次函数来当压轴题，多数采用二次函数，毕竟二次函数综合性较强，但是浙江温州市的最后一道函数综合题，却对一次函数的综合运用，命出了新的高度，原来函数综合，并非二次函数的专属。

题目

如图，在平面直角坐标系中，直线y=-1/2x+4分别交x轴、y轴于点B，C，正方形AOCD的顶点D在第二象限内，E是BC中点，OF⊥DE于点F，连接OE。动点P在AO上从点A向终点C匀速运动，同时，动点Q在直线BC上从某一点Q1向终点Q2匀速运动，它们同时到达终点。

(1)求点B的坐标和OE的长；

(2)设点Q2(m，n)，当n/m=1/7tan∠EOF时，求点Q2的坐标；

(3)根据(2)的条件，当点P运动到AO中点时，点Q恰好与点C重合。

①延长AD长直线BC于点Q3，当点Q在线段Q2Q3上时，设Q3Q=s，AP=t，求s关于t的函数表达式；

②当PQ与△OEF一边平行时，求所有满足条件的AP的长。

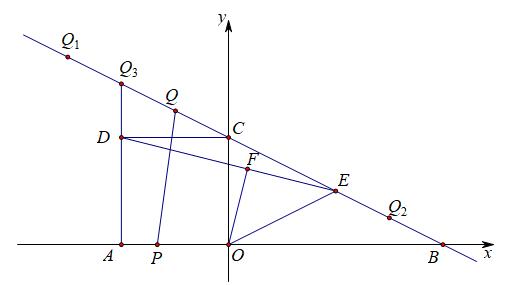
解析：

(1)从已知的一次函数y=-1/2x+4中，我们可以获得很多信息，既能解决第1小题，同时也为后续解题做好准备。首先，它和坐标轴的交点分别是B和C，可分别求出为B(8,0)和C(0,4)，于是我们可以求得BC=4√5，根据直角三角形斜边上的中线等于斜边的一半，求出OE=2√5；

(2)继续研究上小题中的一次函数，正方形AOCD的边长为4，点Q2在这条直线上，意味着n=-1/2m+4，而要求的tan∠EOF恰好处在Rt△EOF中，于是我们只需要求出它对应的两条直角边即可。

方法一：纯解析法，优点是不需要任何辅助线，缺点是计算量较大。

先求出点E坐标(4,2)，D点坐标(-4,4)，可得DE函数解析式为y=-1/4x+3，然后可由OF⊥DE，求出直线OF解析式为y=4x，于是点F坐标可得(12/17,48/17)，然后利用两点距离公式分别求出EF=14√17/17，OF=12√17/17，于是tan∠EOF=7/6，所以n/m=1/6，即m=6n，代入n=-1/2m+4中，解得m=6，n=1，从而得到Q2(6，1)；

方法二：几何法，优点是计算量较小，但需要添加辅助线。

从中点E出发，向y轴作垂线EN，它是△BOC中位线，同时也是△EOM的高，而△EOM还有一条高是OF，这就为使用面积法求线段长埋下伏笔了，如下图：

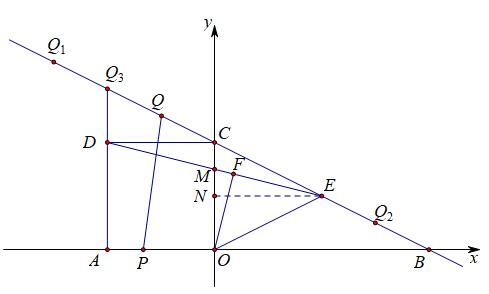
EN是△BOC中位线，因此EN=4，所以很容易证明△CDM≌△NEM，再加上N为OC中点，可得CN=2，于是CM=MN=1，据此求出OM=3，EM=√17，用面积法OM·EN=EM·OF，求出OF=12√17/17，再在Rt△EOF中求出EF=14√17/17，于是tan∠EOF=7/6，所以n/m=1/6，即m=6n，代入n=-1/2m+4中，解得m=6，n=1，从而得到Q2(6，1)；

方法三：代几综合法，优点是既不需要辅助线，计算量也较小。

如下图：

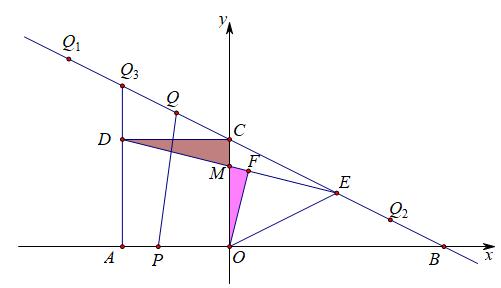
请注意图中那一对相似三角形，△CDM∽△FOM，当然，我们首先还是要求出直线DE的解析式，毕竟D、E两点坐标可求，然后便可求出点M坐标为(0,3)，得到CM=1，OM=3，DM=√17，由相似可得CD:OF=DM:OM，求出OF=12√17/17，再在Rt△EOF中求出EF=14√17/17，于是tan∠EOF=7/6，所以n/m=1/6，即m=6n，代入n=-1/2m+4中，解得m=6，n=1，从而得到Q2(6，1)；

(3)在解决这一小题之前，我们有必要对题目中动点的描述进行深挖理解，关于点P运动，很简单，起点A终点O，路程为4，不妨设速度为单位1，那么点Q呢？速度未知，路程未知，从何而知？

突破口在“它们同时到达终点”和“当点P运动到AO中点时，点Q恰好与点C重合”这两句话上，既然同时到达终点，则意味着点P从OA中点到O，点Q从C点(0,4)到Q2(6,1)，所用时间相同。那么我们先把这两段路程求出来，点P路程为OP=2，点Q路程为CQ2=3√5，因此它们的速度之比VP:VQ=2:3√5，可得VQ=3√5/2·VP，方才我们设VP=1，于是VQ=3√5/2。

解决了速度问题，再来看Q起点问题，Q1到底在哪？

当点P从点A到AO中点时，点Q从Q1到点C，那不和从点C到Q2路程一样吗？刚才我们已经求得CQ2=3√5，于是CQ1=3√5，换句话讲，其实点C是Q1和Q2所连线段的中点，同时Q3坐标可求得，为(-4,6)，于是Q1Q3=3√5-2√5=√5。

①由AP=t，即当速度为单位1时，时间为t，我们可将Q1Q表示出来，为3√5/2t，于是Q3Q=Q1Q-Q1Q3=3√5/2t-√5，即s=3√5/2t-√5；

②从点P运动过程中PQ的位置观察，可知只存在两种情况：PQ∥OF时和PQ∥OE时，由于点Q终点在Q2，因此PQ不可能与EF平行。

(i)当PQ∥OF时，如下图：

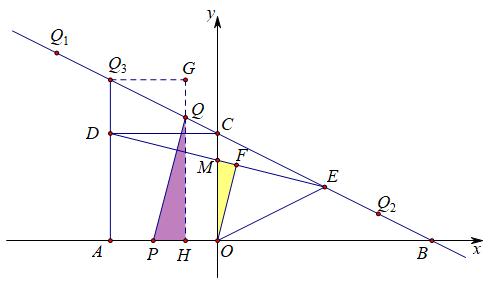
我们过点Q向x轴作垂线GH，过点Q3作GH的垂线交GH于点G。观察△PQH和△MOF，它们都是直角三角形，且∠POH=∠MOF，理由是“如果一个角的两边分别与另一个角的两边平行，那么这两个角相等或互补”，显然直角三角形内角不可能互补，于是它们相等，因此△PQH∽△MOF，而在上一小题中，我们得到它与△CDM相似，取三边比例为1:4:√17（用三角函数方法类似，不再重复），所以△PQH三边之比也为1:4:√17。

然后注意到点Q与点P之间的关联，同样在上一小题中，我们得到的s与t的函数关系，不妨加以利用。依然设AP=t，则Q3Q=3√5/2t-√5，而在Rt△QGQ3中，它与△BOC相似，于是三边之比为1:2:√5，据此求得GQ=3t/2-1，GQ3=3t-2=AH，接下来继续求PH=AH-AP=2t-2，QH=GH-GQ=6-(3t/2-1)=7-3t/2，而PH:QH=1:4，于是列方程为4(2t-2)=7-3t/2，解得t=30/19；

(ii)当PQ∥OE时，如下图：

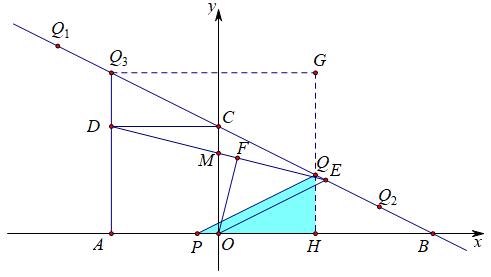
讨论此种情形时，依然利用前一种情形的部分结论，即GQ=3t/2-1，GQ3=3t-2=AH，接下来继续求PH=AH-AP=2t-2，QH=GH-GQ=6-(3t/2-1)=7-3t/2，那么此时的PH和QH比例又是多少呢？观察△PQH和△BOC，其中∠QPH=∠EOH=∠OBC，于是它们相似，因此△PQH的三边比为1:2:√5，因此PH=2QH，于是列方程为2t-2=2(7-3/2t)，解得t=16/5；

综上所述，PQ∥OF时，t=30/19，PQ∥OE时，t=16/5，PQ不可能与EF平行。

解题反思：

这道压轴题最吸引我的地方在于，它是一次函数背景，在全国各地普遍以二次函数压轴的大形势下，是那么的独树一帜，但并非说一次函数压不住轴，恰恰相反，这道题不好解。其难点有二：Q点运动的初始位置未定，P点和Q点运动间的关联。当然，一旦突破这两个难点，那么剩下的便是常规常法了。在解题分析过程中，有几个“经验”可大大减轻思考量，第一个是相似三角形三边比例相同，或者使用三角函数值；第二个是尽量利用已知的、可用的结论。

中考压轴题，能够一开始便思维上路的情况并不多，而是在多次尝试后选择出正确的路，每次尝试失败，但过程中那些有用的结论千万不可放弃，也就是草稿纸的高效利用，在脑子里已经挤满了各种探索思路之后，草稿纸上的蛛丝马迹恰好能帮助找到那条正确的路。

中考压轴题，长期以来各地均不约而同采取二次函数综合题，不排除二次函数本身难度是高于一次函数，但就初中阶段的课标要求，二者地位是相同的，不存在非得使用二次函数作为最后压轴题的说法，事实上，浙江温州这道压轴题是个很好的例子，习惯上用二次函数压轴终归是习惯，而习惯，就是用来打破的，只要能考察出学生对函数综合运用的能力高低，并不在乎用哪种函数，相比之下，一次函数压轴可能更体现出命题者的水平。