H5 如图1，四边形ABCD内接于⊙O，AB=AC，BD⊥AC，垂足为E，点F在BD的延长线上，且DF=DC，连接AF，CF.（1）求证：∠BAC=2∠DAC;（2）若AF=10，BC=4√5，求tan∠BAD的值.

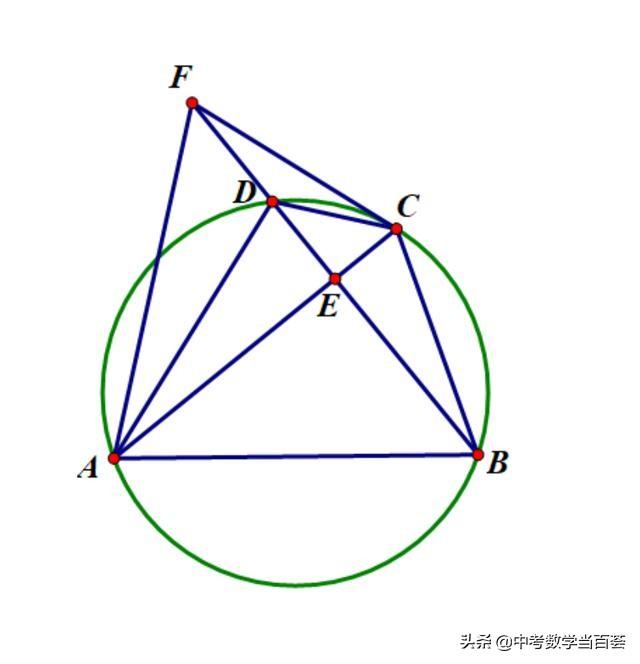
图1

分析

（1）抓住同弧上圆周角相等，BD⊥AC，AB=AC，

进行角的转化，发现所求两角的关系；

（2）分成以下步骤达成目标

第一步：发现CB与CF，AF与AB关系；

第二步：解决圆内接四边形ABCD的边长及对角线长，点E分AC，BD所成的四条线段，

第三步：构造Rt△，利用正切定义求解.

实际操作

（1）弧DC=弧DC=>∠DAC=∠DBC

BD⊥AC=>∠ABD=90°-∠BAC，

∠ACB=90°-∠DBC=90°-∠DAC

∠ABC=∠ABD+∠DBC=90°-∠BAC+∠DAC

AB=AC=>∠ACB=∠ABC=>

90°-∠DAC=90°-∠BAC+∠DAC

=>∠BAC=2∠DAC

（2）DF=DC=>∠DCF=∠DFC=x

=>∠CDB=∠CAB=2x

由（1）知∠BAC=2∠DAC=2x

=>∠DAC=∠DBC= x

∠DFC=∠DBC= x

=>CB=CF=4√5，且AC⊥BD

=>AC垂直平分BE=>AB=AF=AC=10

在Rt△ABE和Rt△CBE中，由勾股定理得

AB^2-AE^2=CB^2-（AC-AE）^2

即100- AE^2=80-（10-AE）^2

解得AE=6,则CE=4，BE=8

在Rt△ADE和Rt△BCE中，

∠DAE=∠CBE=>tan∠DAE= tan∠CBE

=>DE：AE=CE：BE

=>DE=4/8×6=3=>BD=8+3=11，

由勾股定理得AD^2=9+36=45，即AD=3√5

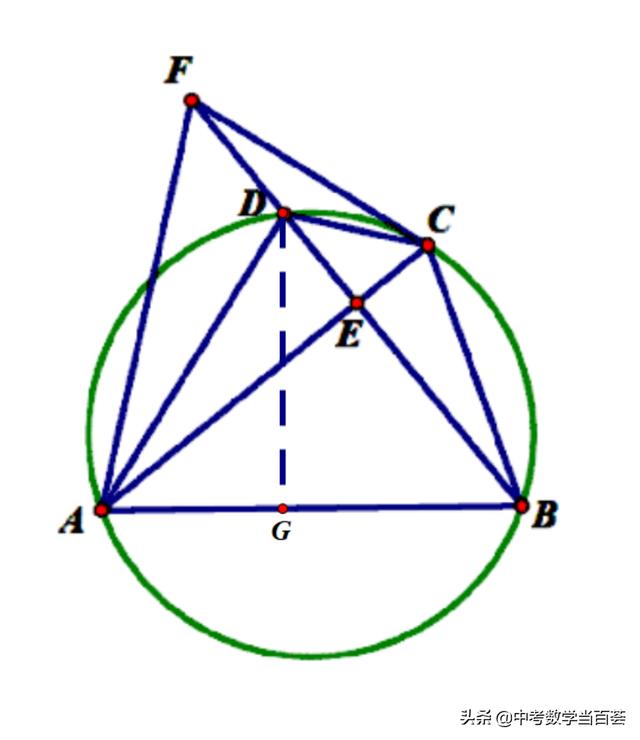
图2

作DG⊥AB，G为垂足（见图2）

在Rt△ADG和Rt△BDG中，由勾股定理得

AD^2-AG^2=BD^2-（AB-AG）^2

即45- AG^2=121-（10-AG）^2

解得AG=6/5,则BG=44/5，DG=33/5

所以tan∠BAD=DG/AG=33/5÷6/5=11/2

综述

本题作为福建今年中考几何压轴题，常规常法，谈不上有多难。但过程繁复，细节琐碎，估计“烦”倒一大批人。

第（1）问，在圆中，主要是利用同弧上圆周角相等，进行角的转换，抓住已知的垂直，等腰关系，发现角之间数量关系，令人眼花缭乱，容易迷失方向，务必紧扣求证的两角，发散思维去找与此相关其他角；

第（2）问，抓住圆内接四边形，对角线互相垂直的特点，反复利用勾股定理建立模型（方程），去求线段长，可以搞定圆内接四边形中所有线段长，这个过程重复两次，解方程，再用勾股定理和相似或三角函数求线段长，还有涉及开方运算等细节处，要反复演算多次，才放心。但期间运算结果不一致时，极易影响情绪而生烦，所以也是对考生心理素质的考验。