江苏宿迁中考数学

宿迁中考数学，选择题最后一题考的是反比例函数K的几何意义、菱形的性质与三角函数的概念，综合性强，计算量大。

8．（3分）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A与原点O重合，顶点B落在x轴的正半轴上，对角线AC、BD交于点M，点D、M恰好都在反比例函数y＝k/x（x＞0）的图像上，则AC/BD的值为（ ）。

【分析】反比例函数常用设点法，将点的坐标假设出来，选用方法不一样，解题的繁琐程度也不一样，提供两种思路对比一下。

两种方法对比可以发现，第二种计算量相对第一种比较小，第二种方法用到了中点坐标公式和两点之间距离公式，两个公式可以参照：2019中考「干货」：一道题带你明白等腰三角形存在性问题

第16题考查的是分式方程中正负解问题，容易出错在忘记去增根。

【分析】本题掌握方法应该不难，先按照解分式方程的正常作法将x求出来，进而利用分式方程的解是正数得出a的取值范围，进而结合分式方程有意义的条件分析得出答案。

18．（3分）如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为（ ）。

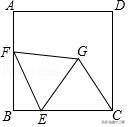
【分析】由题意分析可知，点F为主动点，G为从动点，所以以点E为旋转中心构造全等关系，得到点G的运动轨迹，之后通过垂线段最短构造直角三角形获得CG最小值。

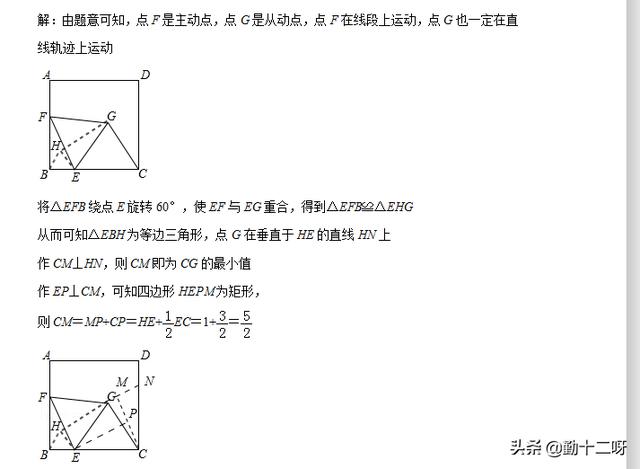
倒数第二题涉及到路径长问题，2019中考数学之路径长问题，你掌握了吗？属于综合性较强的题目，考查了相似三角形的判定和性质，弧长公式，等边三角形的判定和性质，圆周角定理等知识，解题的关键是正确寻找相似三角形解决问题。

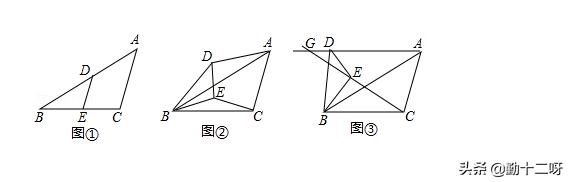
27．（12分）如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．

（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；

（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；

（3）将△BDE从图①位置绕点B逆时针方向旋转180°，求点G的运动路程．

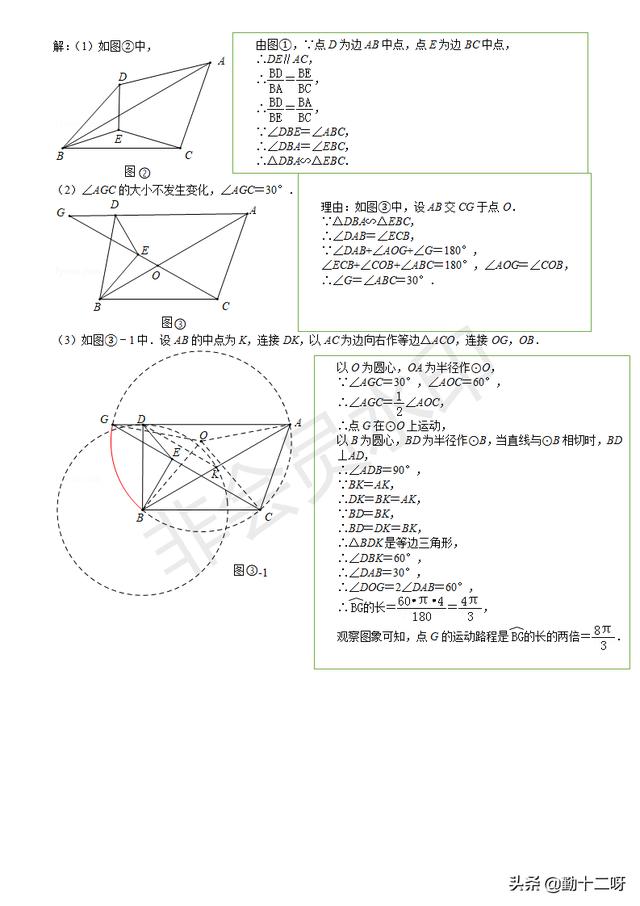
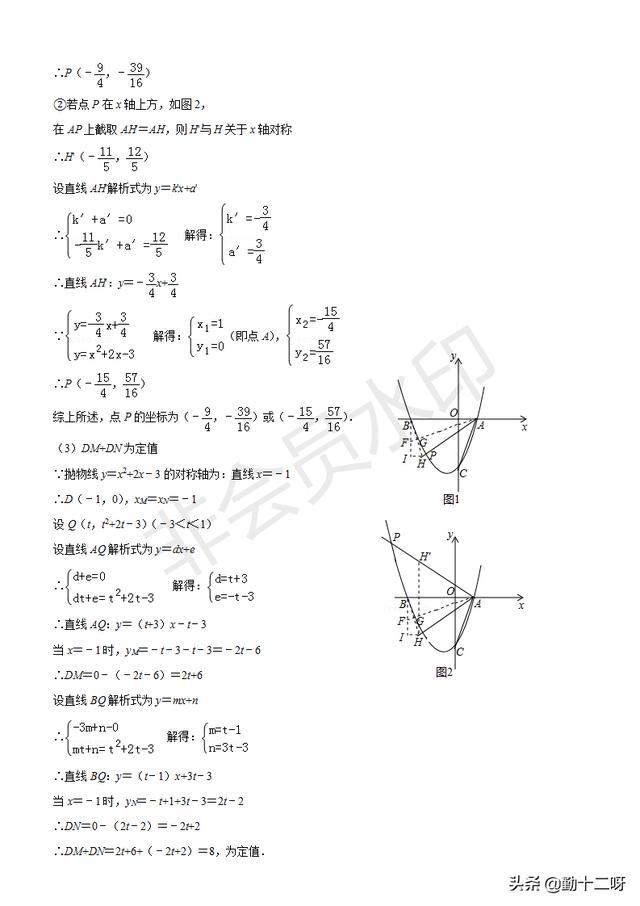
压轴题和盐城卷类似，考察了二次函数角度问题，考查了求二次函数解析式、求一次函数解析式，解一元二次方程、二元一次方程组，等腰三角形的性质，三角函数的应用。第（2）题由于不确定点P位置需分类讨论；（2）（3）计算量较大，应认真理清线段之间的关系再进行计算。