初二全等三角形证明中，初学者常犯的五个易错点

易错点1：找错全等三角形中元素对应关系

例题1：已知AD∥BC，AB∥CD，并且图中的两个三角形全等，请写出它们的对应边与对应角。

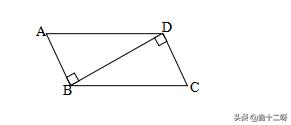
错解：AB与AD，BC与CD，AC与AC；∠BAC与∠DAC，∠B与∠D，∠BCA与∠DCA

正解：AB与CD，AD与BC，AC与AC；∠BAC与∠DCA，∠B与∠D，∠BCA与∠DAC

误区分析：平移、旋转、翻折前后的图形全等，不能只通过对图形的主观印象直接得到结论。比如例题1，不要看了下图，认为△ABC通过翻折可以得到△DAC，那么AB与AD就相等了，其实不然。因此，我们不能主观判断，而要通过分析具体的图形来得到答案。

易错点2：找错对应边、对应角（错用对应边、对应角）

例题2：如图，AC=EF，BC=DE，点A、D、B、F在一条直线上，AD=FB.求证：∠C=∠E

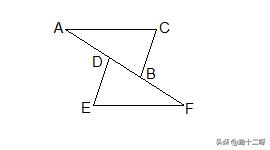
误区分析：我们可以对照着例题2和例题3中的正解和错解看一下，例题2中错解中直接使用了题目中的已知条件AD=FB，但是AD和FB并不是三角形的边；同样的，例题3中直接使用了条件中的∠1=∠2，∠1和∠2同样不是三角形的角。在套用三角形全等的判定定理时，一定要特别注意：所用条件中不要出现不是三角形的边或角这种情况。这是初学者最容易的犯的错误之一。

例题3：如图，AB=AC,AD=AE, ∠1=∠2.求证：∠B=∠C.

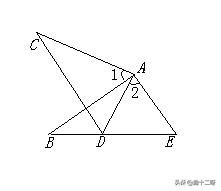
易错点3：忽视由等量关系得到的结论，造成漏解

例题4：如图，AC与BD交于点O，已知△AOD≌△COA，△AOE≌△COF，写出相等的线段．

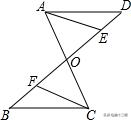
错解：OA=CO,OE=OF,OD=OA,AD=BC

正解：OA=CO,OE=OF,OD=OA,AD=BC，DE=BF

误区分析：例题4中，找相等的线段容易漏掉：DE=BF；找相等的角容易漏掉：∠DAE=∠BCF。这个对应边和对应角不是直接由三角形全等得到的，而是由等边加减等边，等角加减等角得到的，容易遗漏。

易错点4：错用证明全等三角形全等的判定定理

例题5：如图，已知D是△ABC中BC边上一点，且AD⊥BC，E是AD上一点，EB=EC，∠ABE=∠ACE．求证：∠BAE=∠CAE

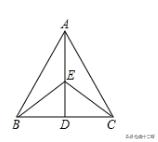
误区分析：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”和HL定理（只适用于直角三角形），运用“SSA”和“AAA”无法判定两个三角形全等。

易错点5：万能的全等三角形

例题6：已知 如图，AB⊥BD，CD⊥BD，AB=DC，求证：AD∥BC.

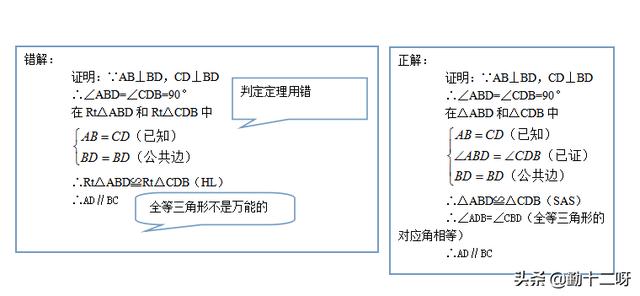
误区分析：错解中是用HL定理来证明三角形全等，这种方法是错误的。HL定理只适用于直角三角形，但是不是直角三角形只能用HL定理来证明，可以发现应该用SAS来证明两个三角形全等。第二个错误也是初学者最容易犯的错误之一：万能的全等三角形。认为无论证什么结论，只要证到两个三角形全等就了事了，全等三角形就是万能的。其实不然，证明平行，我们应该还是要去找内错角相等、同位角相等或同旁内角互补才行，不能单单通过全等得到。两个三角形全等，我们常能得到的结论是：对应边相等、对应角相等。

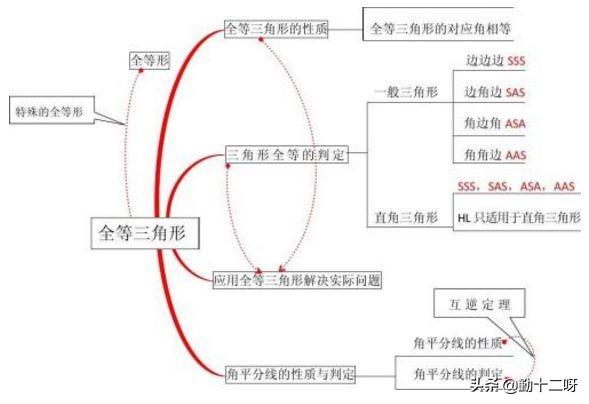
这就是初学者在学习全等三角形常遇到的五个易错点，一定要牢记，不要犯类似的错误。