如图1，平行四边形MNPQ的四个顶点内接于⊙O，MN=4，NP=5，R是NP边上的一个动点，QS⊥MR，垂足为点S，若MR=NP，

（1）求四边形PQRS的周长；

（2）求tan∠SPR的值.

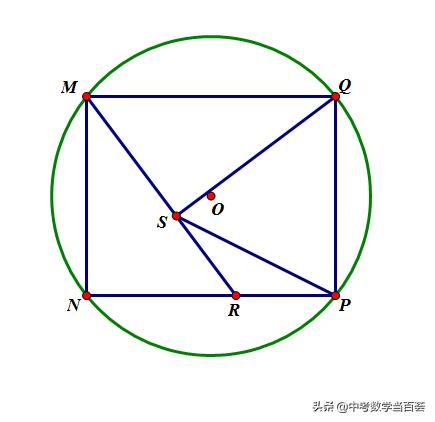
图1

分析

平行四边形MNPQ内接于⊙O＝＞矩形MNPQ

由已知＝＞Rt△MNR≌Rt△QSM＝＞勾股定理得NR=3＝＞求解周长

作ST⊥NP＝＞相似三角形＝＞求ST和TP＝＞tan∠SPR的值

实际操作

MNPQ是⊙O的内接四边形＝＞∠QMN＋∠NPQ=180°

平行四边形MNPQ＝＞∠QMN=∠NPQ

所以∠QMN=∠NPQ=90°＝＞矩形MNPQ

（1）平行四边形MNPQ＝＞MQ∥NP

＝＞∠QMS=∠MRN，若MR=NP=MQ=5

＝＞Rt△MNR≌Rt△QSM

在Rt△MNR中，由勾股定理得NR=3，

所以NR=MS=3，MN=SQ=PQ=4，SR=RP=5－3=2，

四边形PQRS的周长=4＋4＋2＋2=12；

（2）如图2，作ST⊥NP，垂足为T.

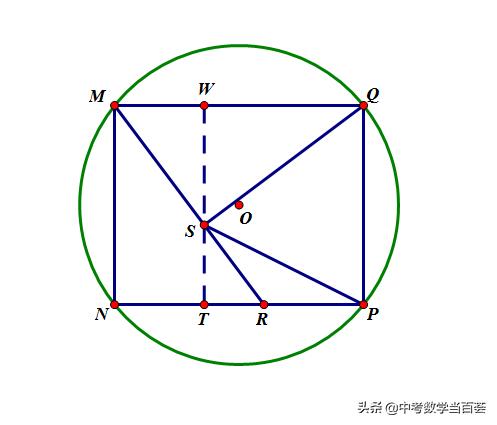
图2

ST∥MN＝＞SR:RM=ST:MN=TR:NR

＝＞2:5=ST:4=TR:3

＝＞ST=8/5，TR=6/5，TP=16/5

＝＞tan∠SPR=ST:TP=1/2

本题知识点：圆内接平行四边形是矩形；圆内接四边形的性质；平行四边形的性质；平行线截线段成比例；相似三角形判定及性质；全等判定及性质；勾股定理；三角函数等。