勾股定理是八年级数学的重点，也是期末考试的必考点，本文就例题详细讲解合理添加辅助线、运用勾股定理解决三角形动点最值问题的解题思路，希望能给大家的期末复习备考提供帮助。

例题

如图，正三角形ABC的边长为2，M是AB边上的中点，P是BC边上任意一点，PA+PM的最大值和最小值分别记作S和T，求S-T的值.

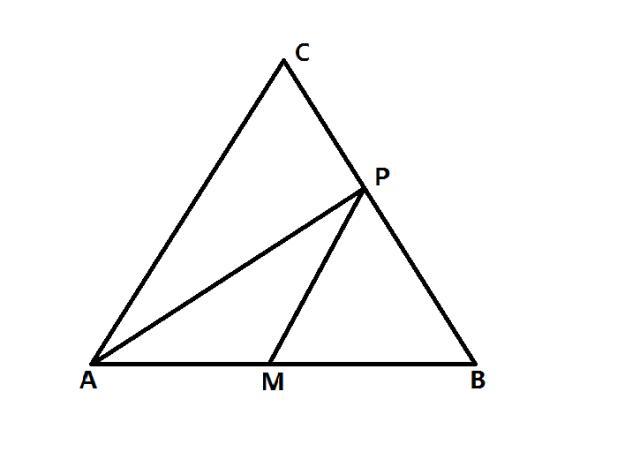
辅助线：以BC为边作∠PBN=60°，使得BN=BM，连接PN，过N作ND⊥AB，交AB的延长线于点D。

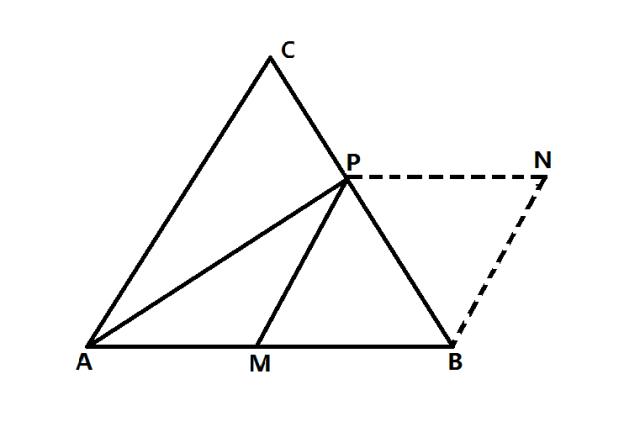
根据全等三角形的判定定理和题目中的条件：两组边及其夹角分别相等的三角形为全等三角形，BN=BM，∠PBN=∠PBM，PB=PB，则△PBN≌△PBM。

根据全等三角形的性质和结论：全等三角形的对应边相等，△PBN≌△PBM，则PN=PM。

根据结论：PN=PM，则PA+PM=PA+ PN。

（1）当P、A、N在同一条直线上时，PA+ PN取到最小值T，T=AN

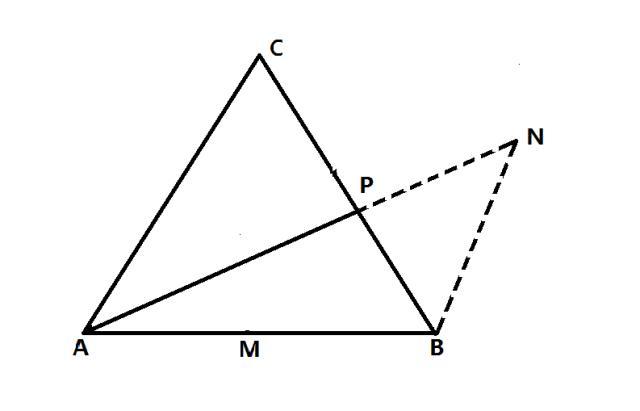
根据题目中的条件：正三角形ABC的边长为2，M是AB边上的中点，则BM=AB/2=1。

根据结论：BN=BM，BM=1，则BN=1。

根据正三角形的性质和题目中的条件：正三角形的每个角为60°，△ABC为正三角形，则∠ABC=60°。

根据题目中的条件和结论：∠DBN+∠ABC+∠PBN=180°，∠PBN=60°，∠ABC=60°，则∠DBN=60°。

根据题目中的条件：ND⊥AB，则∠NDB=90°。

根据题目中条件和结论：∠NDB+∠DBN+∠BND=180°，∠DBN=60°，∠NDB=90°，则∠BND=30°。

根据含30度角直角三角形的性质和结论：在直角三角形中，30度角所对的直角边等于斜边的一半，∠NDB=90°，∠BND=30°，BN=1，则BD=BN/2=1/2。

根据勾股定理和结论：BN=BD+ND，BD=1/2， BN=1，则ND=√3/2。

根据题目中的条件和结论：AB=2，BD=1/2，AD= AB+ BD，则AD=5/2。

根据勾股定理和结论：AN=AD+ND，AD=5/2，ND=√3/2，AN=√7。

所以，PA+ PN的最小值为√7。

（2）当P点与C点重合时，PA+ PN取到最大值S，S=AC+CN

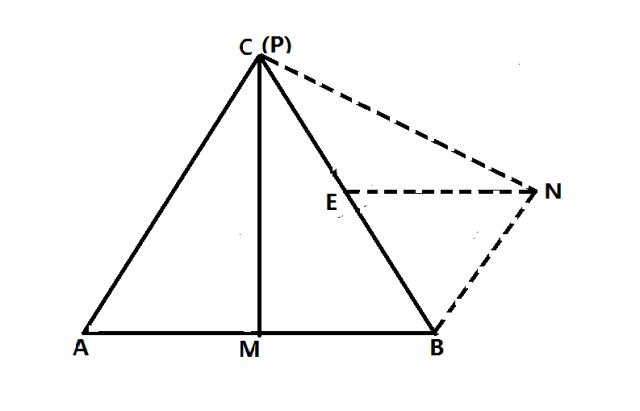
取BC的中点E，连接NE

根据题目中的条件：E为BC的中点，BC=2，则BE=BC/2=1。

根据结论：BE=1，BN=1，则△EBN为等腰三角形。

根据等边三角形的判定定理和结论：一个角为60°的等腰三角形为等边三角形，△EBN为等腰三角形，∠PBN=60°，则△EBN为等边三角形。

根据等边三角形的性质和结论：等边三角形的三边相等，△EBN为等边三角形，则EN=BE。

根据结论： EN=BE，BE=BC/2，则EN= BC/2。

根据直角三角形的判定和结论：一个三角形，如果这个三角形一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形，EN= BC/2，则△PBN为直角三角形，即∠PNB=90°。

根据勾股定理和结论：PB=BN+PN，PB=2，BN=1，则PN=√3。

根据结论：AP=2，PN=√3，则PA+ PN=2+√3。

所以， PA+ PN的最小值为2+√3。

根据结论：T=√7，S=2+√3，则S-T=4√3。

结语

运用勾股定理计算三角形边长的解题思路：

1、合理添加辅助线，构造题目需要求解的线段所在的直角三角形；

2、利用特殊直角三角形的三边关系及题目中的条件，得到构造出来的直角三角形的边长；

3、利用勾股定理进行计算求解。

本文为良师益友谈育儿原创，已加入维权骑士，欢迎转载，请注明出处。