高中物理必修二 | 曲线运动运动合成与分解知识点及例题讲解

一、曲线运动

1.定义：物体运动轨迹是曲线的运动。

2.条件：运动物体所受合力的方向跟它的速度方向不在同一直线上。

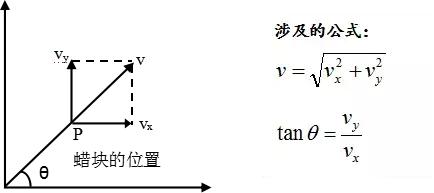
3.特点：①方向：某点瞬时速度方向就是通过这一点的曲线的切线方向。

②运动类型：变速运动（速度方向不断变化）。

③F合≠0，一定有加速度a。

④F合方向一定指向曲线凹侧。

⑤F合可以分解成水平和竖直的两个力。

4.运动描述——蜡块运动

二、运动的合成与分解

1.合运动与分运动的关系：等时性、独立性、等效性、矢量性。

2.互成角度的两个分运动的合运动的判断：

①两个匀速直线运动的合运动仍然是匀速直线运动。

②速度方向不在同一直线上的两个分运动，一个是匀速直线运动，一个是匀变速直线运动，其合运动是匀变速曲线运动，a合为分运动的加速度。

③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。

④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时，合运动是匀变速直线运动，否则即为曲线运动。

三、有关“曲线运动”的两大题型

（一）小船过河问题

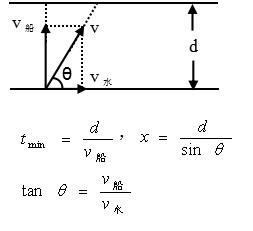
模型一：过河时间t最短：

模型二：直接位移x最短：

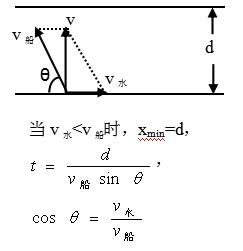
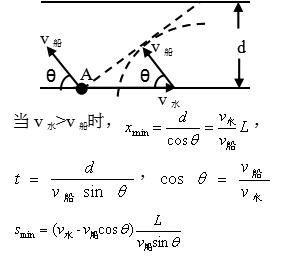
模型三：间接位移x最短：

练 习

1．(2011 年上海卷)如图所示，人沿平直的河岸以速度 v 行走，且通过不可伸长的绳拖船，船沿绳的方向行进．此过程中绳始终与水面平行，当绳与河岸的夹角为α时，船的速率为（ ）。

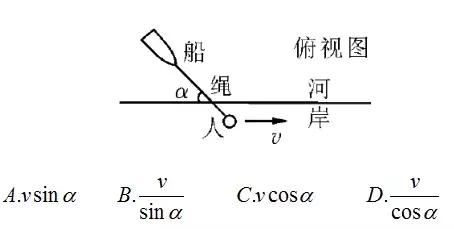
答案解析：

依题意，船沿着绳子的方向前进，即船的速度总是沿着绳子的，根据绳子两端连接的物体在绳子方向上的投影速度相同，可知人的速度 v 在绳子方向上的分量等于船速，故v船＝v cosα，C 正确．

2.(2011 年江苏卷)如图所示，甲、乙两同学从河中O 点出发，分别沿直线游到 A 点和 B 点后，立即沿原路线返回到 O 点，OA、OB 分别与水流方向平行和垂直，且 OA＝OB.若水流速度不变，两人在静水中游速相等，则他们所用时间 t甲、t乙的大小关系为( )

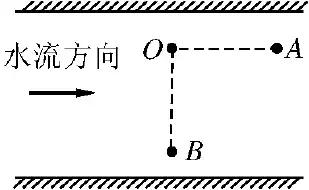
A．t甲<t乙 B．t甲＝t乙

C．t甲>t乙 D．无法确定

（二）绳杆问题(连带运动问题)

1、实质：合运动的识别与合运动的分解。

2、关键：①物体的实际运动是合速度，分速度的方向要按实际运动效果确定；

②沿绳（或杆）方向的分速度大小相等。

模型四：如图甲，绳子一头连着物体B，一头拉小船A，这时船的运动方向不沿绳子。

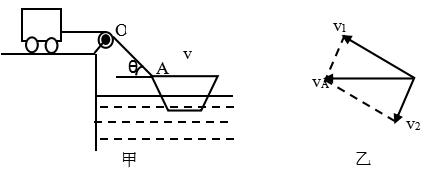
处理方法：如图乙，把小船的速度vA沿绳方向和垂直于绳的方向分解为v1和v2，v1就是拉绳的速度，vA就是小船的实际速度。

练习题

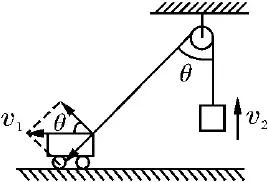
如图，在水平地面上做匀速直线运动的汽车，通过定滑轮用绳子吊起一个物体，若汽车和被吊物体在同一时刻的速度分别为 v1 和 v2，则下列说法正确的是( ）

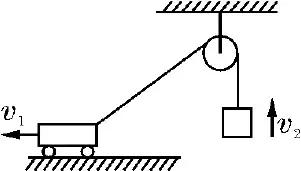
A．物体做匀速运动，且 v2＝v1

B．物体做加速运动，且 v2>v1

C．物体做加速运动，且 v2<v1

D．物体做减速运动，且 v2<v1

解析：汽车向左运动，这是汽车的实际运动，故为汽车的合运动．汽车的运动导致两个效果：一是滑轮到汽车之间的绳变长了；二是滑轮到汽车之间的绳与竖直方向的夹角变大了．显然汽车的运动是由沿绳方向的直线运动和垂直于绳改变绳与竖直方向的夹角的运动合成的，故应分解车的速度，如图，沿绳方向上有速度v2＝v1sin θ.由于v1 是恒量，而θ逐渐增大，所以 v2 逐渐增大，故被吊物体做加速运动，且 v2＜v1，C 正确．