本题来源于2019年宜昌市中考数学第21题，特此说明。

H1.如图1，点O是线段AH上一点，AH=3，以点O为圆心，OA为半径作圆O，过点H作AH的垂线交圆O于C，N两点，点B在线段CN的延长线上，连接AB交圆O于点M，以 AB， BC为边作平行四边形ABCD.

（1）求证：AD是圆O的切线；

（2）若OH=1/3AH，求四边形AHCD与圆O重叠部分的面积；

（3）若NH=1/3AH，BN=5/4,连接MN,求OH,MN的长。

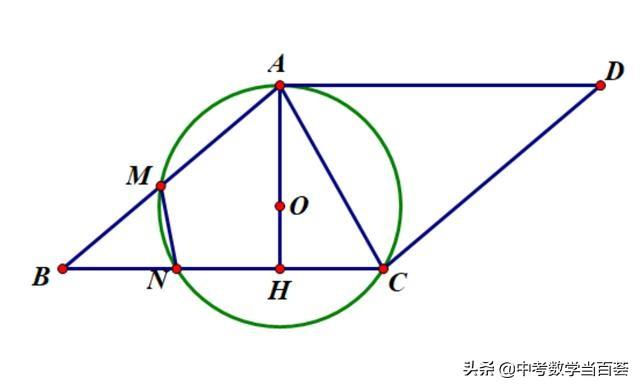
图1

分析

（1）证明AH BC即可；

（2）四边形AHCD与圆O重叠部分的面积=扇形AOC面积+Rt⊿OHC的面积；

（3）利用勾股定理，列方程求OH，利用⊿BMN与⊿BCA相似求MN。

实际操作

(1)平行四边形ABCD=>BC//AD,且AH⊥BC=>OA⊥AD=>AD为⊙O的切线；

(2)连接OC，

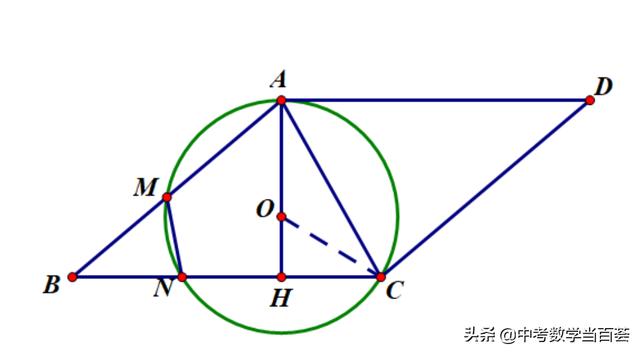
图2

OH=1/3AH，AH=3=>OH=1，半径r=OA=OC=2

=>在Rt⊿OHC和Rt⊿AHC中，

由勾股定理得HC=√3，AC=2√3，∠HOC=60°

=>∠AOC=120°=>扇形AOC的面积=1/3⊙O面积=4π/3，三角形HOC面积=√3/2

=>四边形AHCD与圆O重叠部分的面积=4π/3+√3/2

⑶设OH=x，则半径r=OA=OC=3-x

若NH=1/3AH，BN=5/4，且AH⊥BC=>NH=HC=1，BC=13/4

=>在Rt⊿OHC中，由勾股定理得（3-x）^2-x^2=1=>x=4/3=>OH=4/3

在Rt⊿AHC中，由勾股定理得AC=√10

在Rt⊿ABH中，由勾股定理得AB=15/4

四边形MNCA内接于⊙O=>∠BMN=∠BCA，且∠B=∠B

=>⊿BMN∽⊿BCA=>MN：AC=BN：AB=>MN=√10/3

即此时OH=4/3，MN=√10/3

综述

1.这类几何中档题，主要是利用勾股定理，特殊角三角形边角关系，相似三角形等知识点，建立方程（或直接计算）求解；

2.因为本题圆与平行四边形有关，所以在推理过程中，还要垂径定理，圆内接四边形性质，平行四边形等。