数学思想方法是在数学知识的学习过程中，形成具有独特的解决问题的策略和方法．数学知识的学习是数学思想方法形成的基础，而数学思想对数学知识的学习、理解以及解决问题具有指导意义．

本讲主要学习几个重要的数学思想：“正”、“逆”互化、归纳类比、整体代入、分类讨论、配方构造、待定系数的数学思想方法．

一、核心知识

二、例题解析

（一）、数学公式“正”与“逆”的应用

• 【例1】计算：

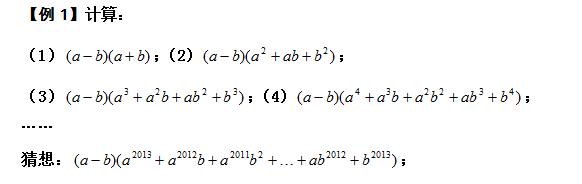
【点拨】正向应用多项式乘法公式，观察每个乘积的结果，得出规律

【解答】

【反思与小结】对于结论探究问题，一般利用“特殊——一般——特殊”的规律，观察最初的结论，从而找到规律，再进行证明。本例观察最初的两个等式或三个等式，猜想规律，再进行证明。

• 【举一反三】计算与化简：

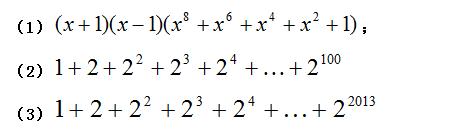
【点拨】对于（1）能否利用例1的结论进行计算与化简？对于（2）、（3）如何将其转化成例1的形式从而应用例1的公式进行解答．

【解答】

• 【例2】

【点拨】“分析法”要求的式子值，要对所求的式子进行通分变形，也要对已知的式子进行变形，变形成次数相同的式子，带入解决。

【解答】

【反思与小结】分析法主要是从结论出发，逆向推理，通过分析要得到结论，需要怎样的条件，从而逐步接近已知条件的分析过程。本例要得到，就要得到，观察已知条件，怎样得到？需要将与的两边分别次方和次方，从而得出解答。

• 【例3】计算：

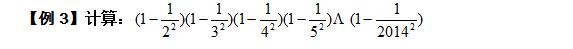
【点拨】思考一：能否从一个因数开始逐步应用“不完全归纳”进行解答？

思考二：观察每个因式的特点，能否“正”或“逆”用平方差公式？应用公式后根据每个因数的特点进行解答？

【解答】

【反思与小结】应用不完全归纳法需要大胆猜想，小心验证与证明。本例既可以根据各因数的特点利用乘法交换律和结合律进行组合解决，又可以利用不完全归纳法进行归纳探究。

• 【举一反三（1）】

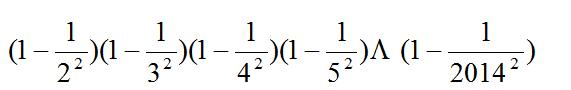
【点拨】能否通过“正”或“逆”用公式化简所求的代数式，然后再证明呢？这也是求代数式的值的常用办法。

【证明】

• 【举一反三（2）】如果m为整数，试说明：m*5-m 能被30整除

【证明】

（二）、利用整体思想化简求值

• 【例4】

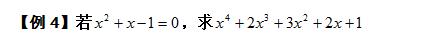
【点拨】“分析法”思考一：要求代数式的值，观察已知条件，能否用含x的一次代数式分别表示出所求式子中的每一项，再进行化简求解呢？这种“各个击破”的方法是解决此问题的关键。

思考二：要求代数式的值，能否将已知的条件作为一个整体代入求解？这种整体代入的方法也是一种常用方法。

【解答】

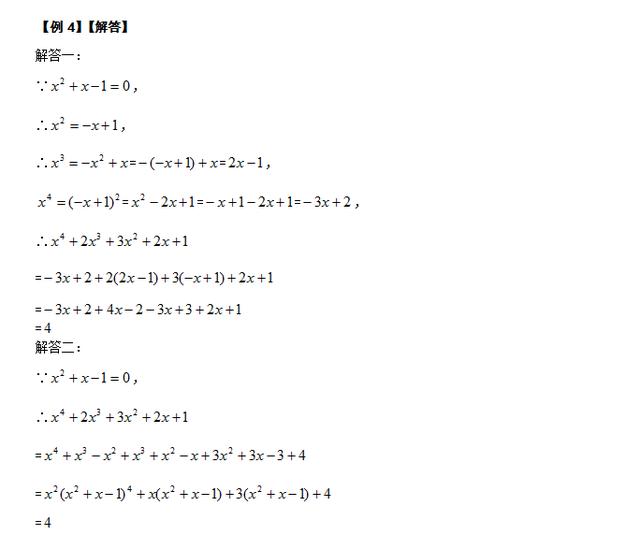
【反思与小结】对于含“零值多项式”的问题一般将要求代数式当成被除式，“零值多项式”作为除式，将要求代数式写成“被除式=除式×商式+余式”的形式，一般的余式为已知常数。从而得出解答。也可以根据“零值多项式”的特点，用含多项式中字母的一次式表示高次式，采取逐步“降次代入”，从而得出解答。本例采用两种方法均可。

• 【举一反三】

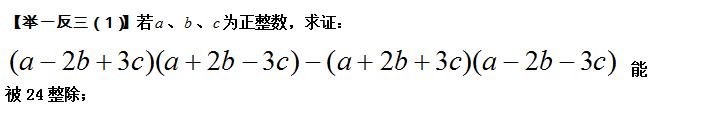
【点拨】本题的解决策略与例4一样，可以考虑“各个击破”法。

【解答】

（三）、“整体思想”、“待定系数法”的初步应用

• 【例5】

【点拨】思考一：根据题意列出算式，能否根据对应项的系数相等解决问题？

思考二：能否用“方程、等式”的观点分析解决？观察得到的方程解有何特点？能否代入几个特殊解进行解答？

【解答】

【反思与小结】解决多项式的整除、含因式问题一般有两种解决策略。第一种：利用待定系数法写成等式形式，利用对应系数相等，解决问题；第二种：写成等式形式，对于含未知数的等式看成方程，而这个方程有无数个解（每个数都是它的解），可以利用几个特殊的数进行解答。

• 【例6】如果多项式能够被整除，求的值

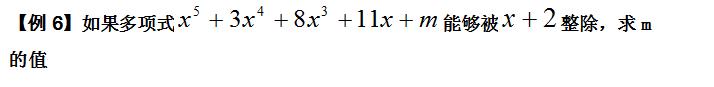
【点拨】根据已知条件将其转化成等式形式解答．

【解答】

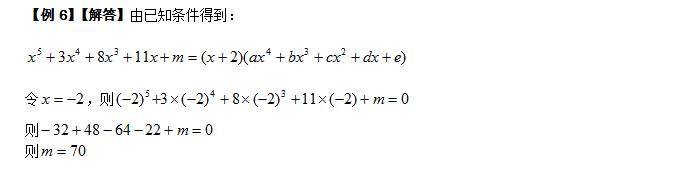
【反思与小结】本例既可以利用待定系数法又可以应用等式方程法解答。

（四）、完全平方数的构造与证明

• 【例7】观察一列数：

49，4489，444889，44448889，4444488889，………，

这列数中的每个数是否是完全平方数？如果是，请说明它们是完全平方数的理由．

【点拨】观察49=7*2，能否得到4489=（ ）2？作出猜想，思考如何表示这列数？如何证明它们是完全平方数？

【解答】

【反思与小结】对于猜想验证或证明完全平方式的问题，一般采用字母表示要验证的式子，从而利用多项式的完全平方式解决问题。解答此类问题，主要注意的应用。

（五）、整除问题的验证与证明（以下例题为选讲内容）

【例8】若m为正整数，求证：m*3+11m必定能被6整除；

【点拨】“分析法”要证明能被6整除，只要证明能被2整除和能被3整除即可．

对于能被2整除，只要说明是偶数即可；对于能被3整除，则需要分类说明能被3整除，则问题解决．

【解答】

【反思与小结】对于含m多项式能被具体数字n整除的问题的解决策略是分类讨论，将m分成n类，分类讨论，分别进行证明，从而问题得证。

• 【举一反三】若正整数a、b、c满足a*2+b*2=c*2，且a、b、c的最大公约数为1，

①试说明：a、b、c中至少有一个能被3整除；

②试说明：a、b、c中至少有一个能被5整除；

【点拨】要证明：a、b、c中至少一个能被3整除，不容易证明，能否假设a、b、c都不能被3整除，推出矛盾，从而说明a、b、c中至少一个能被3整除？进一步思考：正整数a、b、c被3除的余数如何表示？有几种情况？能否对每种情况分析讨论？

同样方法证明：a、b、c中至少有一个能被5整除；

【解答】

【课后练习】①若a为奇数，说明：a*2被8除的余数是1；

②利用①证明：若正整数a、b、c满足a*2+b*2=c*2，且a、b、c的最大公约数为1，

试说明：a、b、c中至少有一个能被4整除；

三、积累与反思

本讲主要学习了公式的“正”、“逆”的应用以及归纳类比、整体代入、分类讨论、配方构造、待定系数的数学思想方法。关于多项式的理论中含有的数学思想方法比较广泛，在进行恒等式变形时，要注意应用数学思想方法解决问题，从而提高解决问题的能力。