一次函数与反比例函数是八年级的重要知识点，利用函数方法解决几何图形的计算问题是期末考试的难点，本文就例题详细讲解这类题型的解题思路，希望能给大家期末复习备考带来帮助。

例题

如图，在平面直角坐标系中，一次函数=-4/3x+4的图像与x轴、y轴分别相交于点C、D，四边形ABCD是正方形，反比例函数y=k/x的图像在第一象限经过点A。

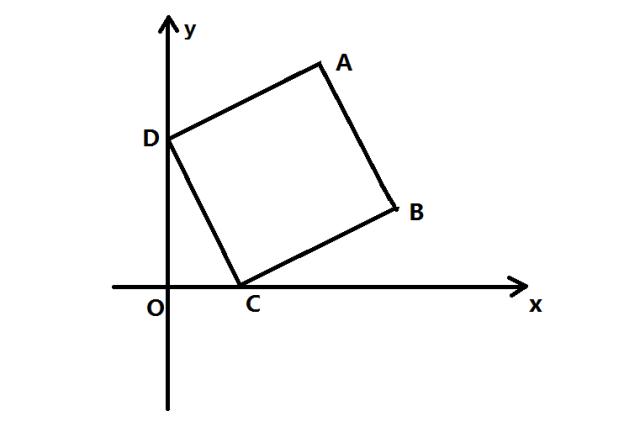
（1）求点A的坐标及k的值；

（2）点P是反比例函数y=k/x（x>0）的图像上一点，且△PAO的面积为21，求点P的坐标。

1、求点A的坐标及k的值

根据题目中的条件：点C、D在一次函数=-4/3x+4的图像上，则当x=0时，解得y=4，当y=0时，解得x=3，即C点坐标为（3,0）、D点坐标为（0,4）。

过A点作AE⊥y轴，交y轴于点E

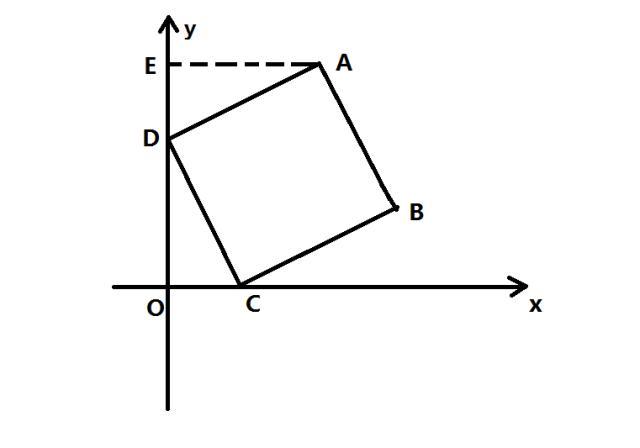
根据正方形的性质和题目中的条件：正方形的四条边相等，四个角为直角，四边形ABCD是正方形，则AD=DC，∠ADC=90°。

根据题目中的条件和结论：∠ADE+∠ADC+∠CDO=180°，∠ADC=90°，则∠ADE+∠CDO=90°。

根据题目中的条件和结论：∠COD+∠OCD+∠CDO=180°，∠COD=90°，则∠OCD+∠CDO=90°。

根据结论：∠ADE+∠CDO=90°，∠OCD+∠CDO=90°，则∠ADE=∠OCD。

根据辅助线：AE⊥y轴，则∠AED=90°。

根据题目中的条件和结论：∠ADE+∠AED+∠DAE=180°，∠AED=90°，则∠ADE +∠DAE=90°。

根据结论：∠ADE +∠DAE=90°，∠ADE+∠CDO=90°，则∠DAE=∠CDO。

根据全等三角形的判定定理和结论：两角及其夹边分别相等的两个三角形全等，∠DAE=∠CDO，AD=DC，∠ADE=∠OCD，则△ADE≌△DCO。

根据全等三角形的性质和结论：全等三角形的对应边相等，△ADE≌△DCO，则AE=DO，DE=CO。

根据结论：C点坐标为（3,0）、D点坐标为（0,4），则CO=3，DO=4。

根据结论：AE=DO，DE=CO，CO=3，DO=4，，则AE=4，DE=3。

根据题目中的条件和结论：DO=4，DE=3，OE=DO+DE，则OE=7。

所以，A点坐标为（4,7）。

根据题目中的条件和结论：A点在反比例函数图像上，A点坐标为（4,7），则把A点坐标代入y=k/x能使等式成立，即7=k/4，可解得k=28。

2、求点P的坐标

设点P的坐标为（a,28/a）

当P在A的下方

过A点作AF⊥x轴，交x轴于点F，过P点作PG⊥x轴，交x轴于点G

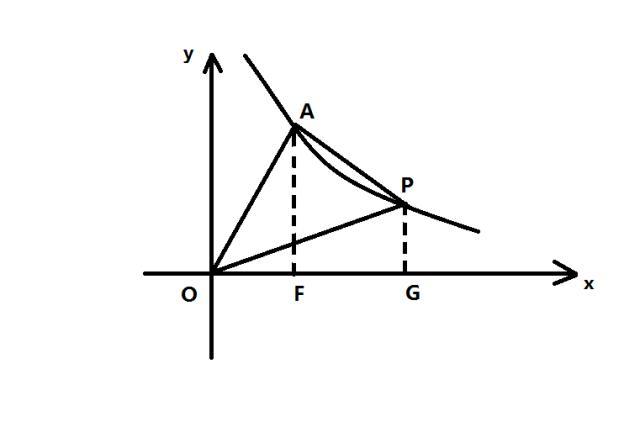
根据辅助线：AF⊥x轴，PG⊥x轴，则△AOF、△POG为直角三角形，。

根据平行线的判定定理和辅助线：垂直于同一直线的两直线平行，AF⊥x轴，PG⊥x轴，则四边形AFGP为直角梯形。

根据结论：A点坐标为（4,7），P点坐标为（a,28/a），则AF=7，OF=4，OG=a，PG=28/a，FG=a-4。

根据三角形的面积计算公式和结论：S△AOF=AF*FO/2，AF=7，OF=4，则S△AOF=14。

根据梯形的面积计算公式和结论：S梯形AFGP=（PG+AF）*FG/2，AF=7，PG=28/a，FG=a-4，则S梯形AFGP=（7+28/a）（a-4）/2。

根据三角形的面积计算公式和结论：S△POG=PG*OG/2，AF=7，OF=4，则S△POG=14。

根据题目中的条件和结论：S△PAO=S△AOF+S梯形AFGP-S△POG，S△AOF=14，S梯形AFGP=（7+28/a）（a-4）/2，S△POG=14，则S△PAO=7a/2-56/a。

根据题目中的条件和结论：S△PAO=21，S△PAO=7a/2-56/a，则a=8或a=-2。

根据题目中的条件：点P在第一象限，则a=-2不符合条件，舍去，即a=8符合题意，即P点坐标为（8,7/2）。

过A点作AM⊥y轴，交y轴于点M，过P点作PN⊥y轴，交y轴于点N

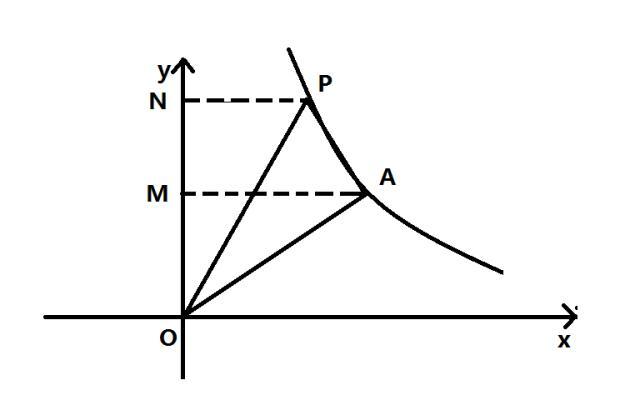
根据辅助线：AM⊥y轴，PN⊥y轴，则△AOM、△PON为直角三角形，。

根据平行线的判定定理和辅助线：垂直于同一直线的两直线平行，AM⊥y轴，PN⊥y轴，则四边形AMNP为直角梯形。

根据结论：A点坐标为（4,7），P点坐标为（a,28/a），则AM=4，OM=7，ON=28/a，PN=a，NM=28/a-7。

根据三角形的面积计算公式和结论：S△AOM=AM*MO/2，AM=4，OM=7，则S△AOM=14。

根据梯形的面积计算公式和结论：S梯形AMNP=（PN+AM）*NM/2，AM=4，PN=a，NM=28/a-7，则S梯形AMNP=（28/a-7）（a+4）/2。

根据三角形的面积计算公式和结论：S△PON=PN*ON/2，ON=28/a，PN=a，则S△PON=14。

根据题目中的条件和结论：S△PAO=S△AOM+S梯形AMNP-S△PON，S△AOM=14，

S梯形AMNP=（28/a-7）（a+4）/2，S△PON=14，则S△PAO=56/a-7a/2。

根据题目中的条件和结论：S△PAO=21，S△PAO=56/a-7a/2，则a=-8或a=2。

根据题目中的条件：点P在第一象限，则a=-8不符合条件，舍去，即a=2符合题意，即P点坐标为（2,14）。

所以，P点坐标为（8,7/2）或（2,14）时，△PAO的面积为21。

结语

利用函数方法解决几何图形的计算问题的解题思路：

1、由函数关系式得到几何图形上某些特殊点的坐标值；

2、利用这些坐标值确定几何图形在直角坐标系中的位置；

3、利用几何图形的性质得到几何图形上其他关键点的坐标值；

4、把无法直接求解的图形面积转换为可以求解的几个图形的面积和或差进行计算。

本文为良师益友谈育儿原创，已加入维权骑士，欢迎转载，请注明出处。