“三兄弟”——平行线、角平分线和等腰三角形经常会在平行四边形这一章进行运用,是必须要熟练掌握的模型,作为组合类辅助线,看见其二,还要想到构造另外一个,考察最多的是平行线+角平分线,延长法构造等腰三角形.
下面让我们一起来研究下:
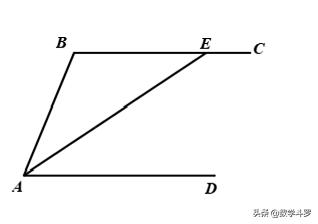
一、 平行线+角平分线
如图,AD∥BC,AE平分∠BAD,则AB=BE.
∵AD∥BC
∴∠EAD=∠BEA
∵AE平分∠BAD
∴∠BAE=∠EAD
∴∠BAE=∠BEA
∴AB=BE

二、 角平分线+等腰三角形
如图,AE平分∠BAD,AB=BE,则AD∥BC.
∵AE平分∠BAD
∴∠BAE=∠EAD
∵AB=BE
∴∠BEA=∠BAE
∴∠BEA=∠EAD
∴AD∥BC

三、平行线+等腰三角形
如图,AD∥BC,AB=BE,则AE平分∠BAD.
∵AD∥BC
∴∠BEA=∠EAD
∵AB=BE
∴∠BAE=∠BEA
∴∠BAE=∠EAD
∴AE平分∠BAD
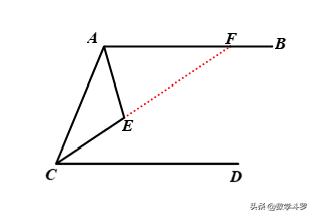
四、平行线+角平分线(辅助线)
延长法(延长角平分线)构造等腰三角形
如图,AB∥CD,CE平分∠ACD,则
延长CE交AB于点F,
易得:△ACF是等腰三角形.
结语:
平行线,角平分线,等腰三角形就像三兄弟,他们形影不离,题目中出现其中二个,要想到另外一个,如果没有,可以通过添加辅助线得到另外一个。只有熟练掌握了,我们才能提高做题效率。
练习:
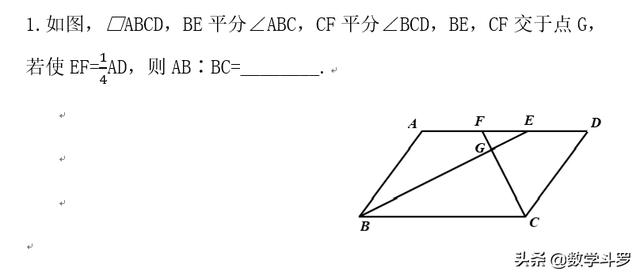
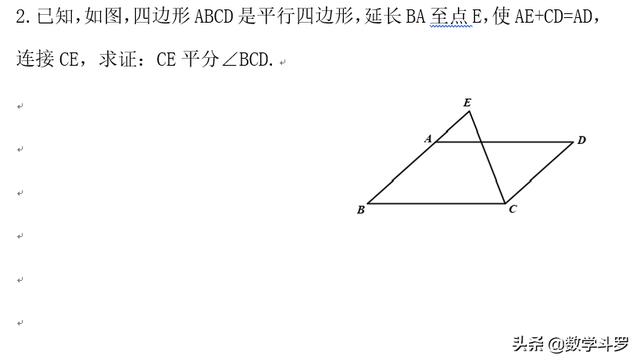

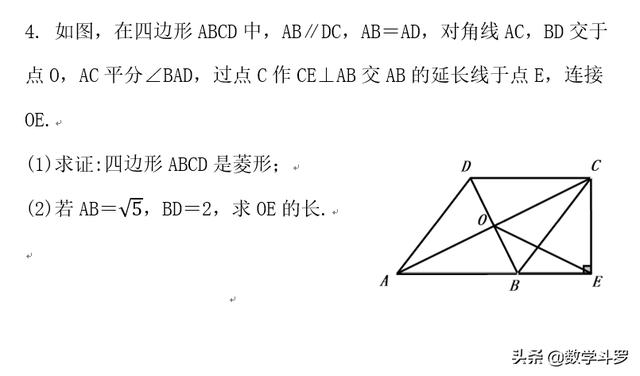
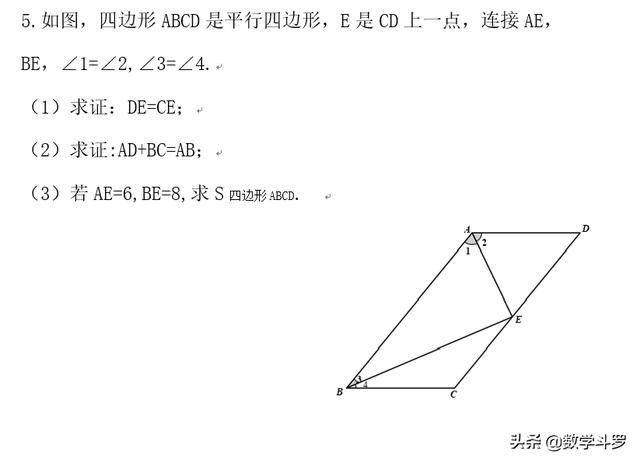

 加载中,请稍侯......
加载中,请稍侯......
精彩评论