中考数学压轴题：抛物线上平行四边形找不到？掌握方法直接求

中考数学的最后一题是压轴大题，通常是二次函数与几何的结合，难度较大，计算复杂，是学生最容易失分的地方。2019年山西省中考数学就是这样。我们先来看一下题吧。

中考压轴题

第1问和第2问都是常规题，在固定的解题法，只要认真计算，就可以做对，在这里不作讲解。我想重点讲的是第3问，如何在抛物线上寻找平行四边形。这是一个动点问题，许多同学一看动点，头就变大，感觉无从下手，没有思路。这是因为同学们没有抓住关键点，找不到突破口。如果能够抓住关键点，问题就迎刃而解了。

我们来看一下第三个问题。

（3） 在（2）的条件下，若点M是x轴上的一动点，点N是抛物线上的一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出M点的坐标；若不存在，请说明理由。

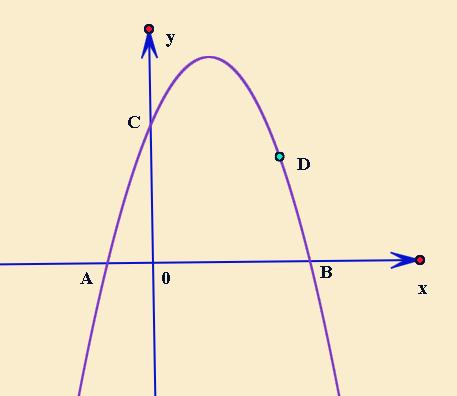
第3问

也就是知道两个定点B和D，然后找两个动点M和N，M在x轴上，N在抛物线，使得以点B，D，M，N为顶点的四边形是平行四边形。只有找出平行四边形，知道两个动点是怎么确定的，我们才能进行计算。那么知道两个点，怎么去找平行四边形呢？

首先我们要知道两个定点的连线是平行四边形中的什么，只有两种情况，一种是平行四边形的一条边，另一种是平行四边形的对角线。

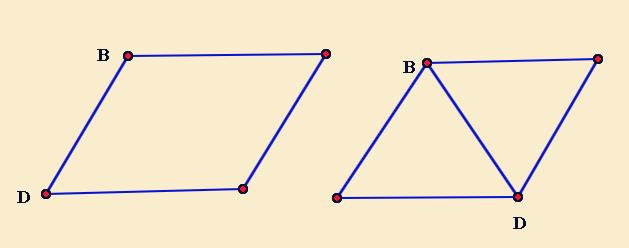
两定点连线的两种情况

知道了这两种情况，我们就知道要分情况进行讨论。

1、如果BD是平行四边形的一条边。

如果BD是平行四边形的一条边，那么MN就是它的对边，根据平行四边形的性质，就要求BD平行且等于MN，其实质，就是将BD平行，使其一个端点在x轴上，一个端点在抛物线上。

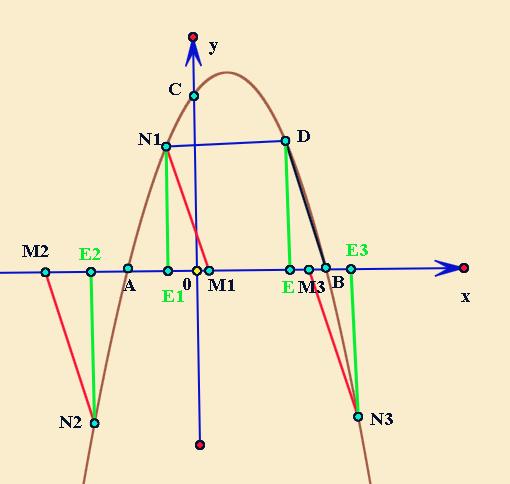
如图所示，通过平移，我们可以得到三条符合条件的线段：N1M1，N2M2，N3M3。

找到了平行四边形的顶点，接下来，我们就要去求两动点的坐标了。

我们分别做D，N1，N2，N3到X轴的垂线段DE，N1E1，N2E2，N3E3，根据平行四边形的性质，会发现DE=N1E1=N2E2=N3E3，都等于D点纵坐标的绝对值，也就是知道动点N的纵坐标，接下来就可以求出横坐标了。同时，根据平行四边形的性质，我们也可发现，BE=M1E1=M2E2=M3E3，从而我们可以求出M点的坐标。

2、如果BD是平行四边形的对角线。

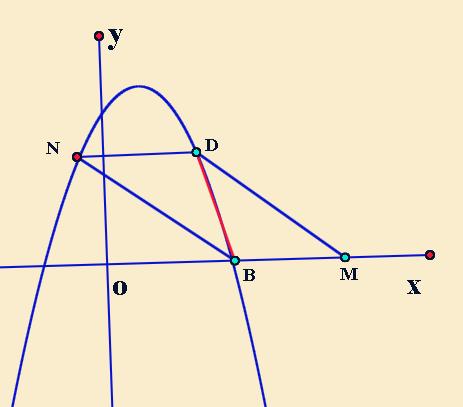
如果BD是对角线，那么BM和NE就是两组对边，BM在X轴上，那么ND平行X轴。所以，过D点作X轴的平行线，与抛物线的交点就是N，再作BM=ND，就找到M点。其实是算ND的长度。我们可以计算出N点的横坐标来算，也可以用抛物线的对称性来算。

经上分析，当我们遇到这样一类题：两个定点A，B，A点在抛物线上，B点是抛物线与X轴的一个交点，两个动点M和N，M在X轴上运动，N在抛物线上运动，求点M，N，使A，B，M，N为顶点的四边形是平行四边形。我们可以不需要求点，直接求了。

1、求出A点的纵坐标，算出A，B两点横坐标的差距。

2、将A点的纵坐标代入抛物线解析式中求解，得出N点的横坐标。横坐标加上或减去A，B两点横坐标的差距，求出M点的坐标。

3、将A点的纵坐标的相反数代入抛物线的解析式中求解，得出另外的N点的横坐标，横坐标加上或减去A，B两点横坐标的差距，求出M点的坐标。

4、找出A点在抛物线上的对称点N，利用抛物线的对称性，算出AN的长度，用B点的横坐标加上或减去A，B两点横坐标的差距，求出M点的坐标。