例题1

【常规解法】

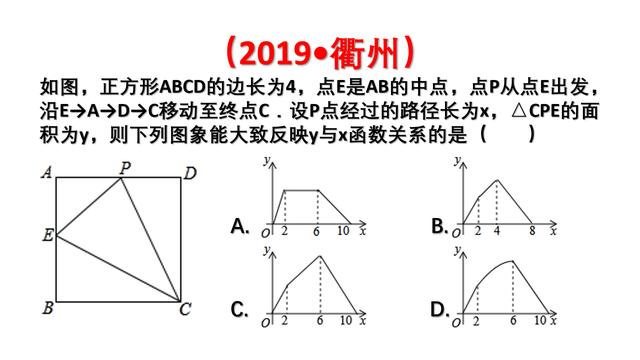
【分析】根据题意分类讨论，随着点P位置的变化，△CPE的面积的变化趋势．

解：通过已知条件可知，当点P与点E重合时，△CPE的面积为0；

当点P在EA上运动时，△CPE的高BC不变，则其面积是x的一次函数，面积随x增大而增大，

当x=2时有最大面积为4，

当P在AD边上运动时，△CPE的底边EC不变，则其面积是x的一次函数，面积随x增大而增大，

当x=6时，有最大面积为8，当点P带DC边上运动时，△CPE的底边EC不变，则其面积是x的一次函数，面积随x增大而减小，最小面积为0；故选：C．

【点击本质】

解：由题意知，点P运动轨迹AE+AD+CD=10，故排除B。

当2<x<6时，P在AD边上运动，△CPE的底边EC不变，则其面积是x的一次函数，面积随x增大而增大，故排除A、D。故正确选项为C。

例题2

【常规解法】

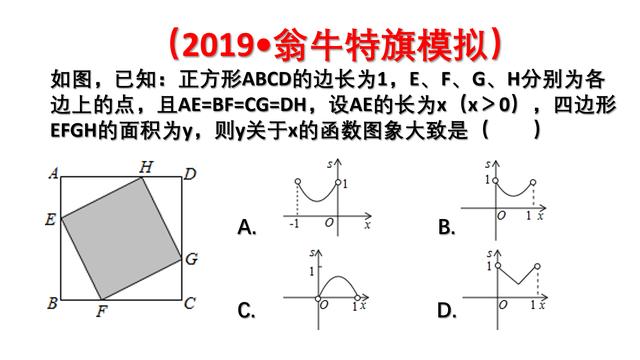
【分析】根据条件可知△AEH≌△BFE≌△CGF≌△DHG，设AE为x，则AH=1-x，根据勾股定理EH2=AE2+AH2=x2+（1-x）2，进而可求出函数解析式，求出答案．

解：∵根据正方形的四边相等，四个角都是直角，且AE=BF=CG=DH，

∴可证△AEH≌△BFE≌△CGF≌△DHG．

设AE为x，则AH=1-x，根据勾股定理，得

EH2=AE2+AH2=x2+（1-x）2

即y=x2+（1-x）2．

y=2x2-2x+1，

∴所求函数是一个开口向上，

对称轴是直线x=1/2

∴自变量的取值范围是大于0小于1．

故选：B．

【点击本质】

解：x>0，故排除A。

由题意知，EFGH面积随着AE=x增加，先变小，再变大，故排除C。

另一方面，由于y表示EFGH面积，我们知道，面积是二维变量，它应为边长的二次函数，于是y与x应为抛物线图像，故正确选项为B。

小结

通过以上例题．可以得出解决这类问题的一般步骤：

第一步：弄清题意，分析函数自变量的取值范围及分段；

第二步：分析各段上的函数的变化趋势；

第三步：确定函数的解析式的形式，根据函数的性质选出正确答案。

在整个解题过程中，应坚持选择题的解决思想：”为达目的，不择手段“，只要选出正确答案即停。

那么，按照这种思路结合以上两道例题的点击本质环节可知，我们对于这类型题往往可以深入分析函数与自变量的关系，尤其是次数的考察，应尽量避免花大力气寻求函数关系式而使得小题大做。

真题演练

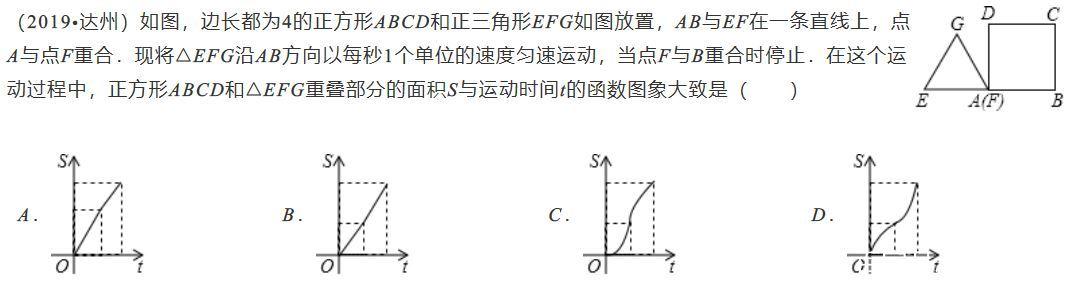
选C