如图，KM是平行四边形KLMN的对角线，∠LKM＝∠NKM.

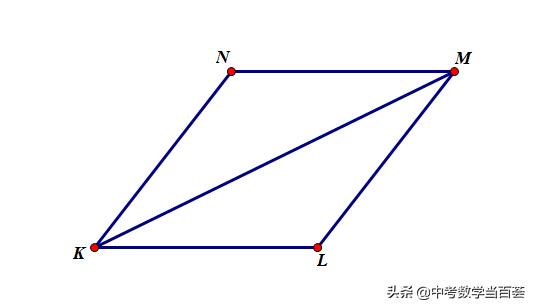
（1）求证：KL＝LM；

（2）若KL＝2，KM＝2，求平行四边形KLMN的面积．

分析

（1）等角对等边＝＞KL＝LM；

（2）证明KLMN是菱形，利用菱形面积公式求解.

实际操作

（1）∵四边形KLMN是平行四边形，

∴KN∥LM，

∴∠NKM＝∠LMK，

∵∠LKM＝∠NKM，∴∠LKM＝∠LMK，

∴KL＝LM；

（2）连接LN交KM于O，

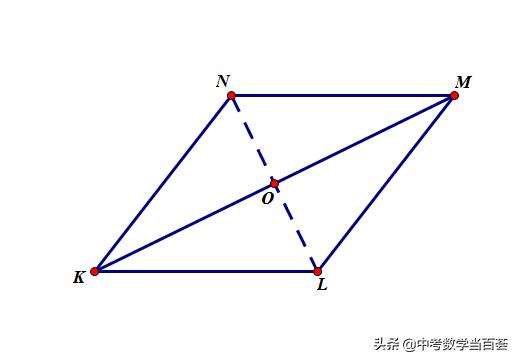
∵四边形KLMN是平行四边形，KL＝LM，

∴四边形KLMN是菱形，

∴KM⊥LN，OK＝OM＝1/2KM＝√3，

OL＝ON＝1/2LN，

∴OL^2＝KL ^2－OK ^2=4－3=1

∴OL＝1，

∴LN＝2OL＝2，

∴平行四边形KLMN的面积＝

KM·LN/2＝1/2×2×2＝2.

综述

1.本题是中考的几何基础题，主要考查平行四边形的性质，菱形的判定，勾股定理，菱形的性质及面积计算，分值6~7分。