图形的旋转有三个要素：①旋转中心； ②旋转方向； ③旋转角度．三要素中只要任意改变一个，图形就会不一样．

旋转具有以下性质：

①对应点到旋转中心的距离相等，即边相等。

②对应点与旋转中心所连线段的夹角等于旋转角，即角相等

③旋转前、后的图形全等。

以这三个性质为突破口，就能快速解决问题。

图形的旋转在中考中可能有三种出题方式，今天我们以下面几道试题为例研究一下旋转试题的解题技巧。

选择题

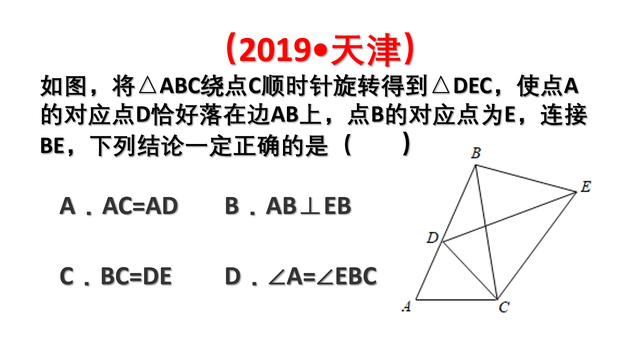
【分析】根据旋转的性质得到AC=CD，BC=CE，AB=DE，故A错误，C错误；

得到∠ACD=∠BCE，根据三角形的内角和得到∠A=∠ADC=（180°-∠ADC）/2，∠CBE=（180°-∠BCE）/2求得∠A=∠EBC，故D正确；由于∠A+∠ABC不一定等于90°，于是得到∠ABC+∠CBE不一定等于90°，故B错误．

【解答】

【点评】本题考查了旋转的性质，等腰三角形的性质，正确的识别图形是解题的关键．

填空题

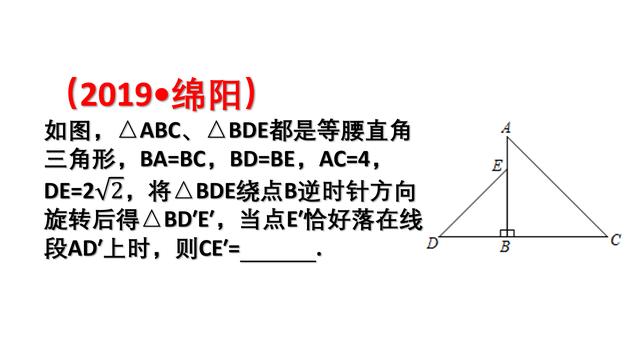
【分析】连接CE′，根据等腰三角形的性质得到AB=BC=2√2，BD=BE=2，根据性质的性质得到D′B=BE′=BD=2，∠D′BE′=90′，∠D′BD=∠ABE′，由全等三角形的性质得到∠D′=∠CE′B=45°，过B作BH⊥CE′于H，解直角三角形即可得到结论．

【解答】

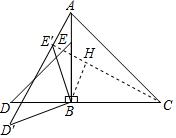
【点评】本题考查了旋转的性质，全等三角形的判定和性质，等腰直角三角形的性质，解直角三角形，正确的作出辅助线是解题的关键．

解答题

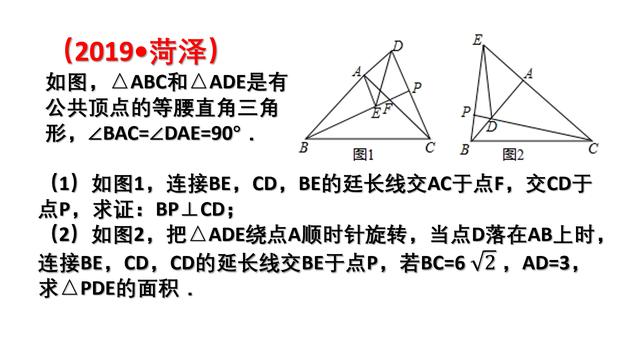
【分析】

（1）根据等腰直角三角形的性质得到AD=AE，AB=AC，∠BAC-∠EAF=∠EAD-∠EAF，求得∠BAE=∠DAC，根据全等三角形的性质得到∠ABE=∠ACD，根据余角的性质即可得到结论；

（2）根据全等三角形的性质得到∠ABE=∠ACD，BE=CD，求得∠EPD=90°，得到DE=3√2，AB=6，求得BD=6-3=3，CD=√(AD2+AC2）=3√5，根据相似三角形的性质得到PD=√5/5，PB=6√5/5，根据三角形的面积公式即可得到结论．

【解答】

（1）略

（2）

【点评】本题考查了旋转的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，等腰直角三角形的性质．熟练掌握旋转的性质是解题的关键．

小结

对于旋转问题，

首先，我们要观察图形，看看这个图形的旋转中心，找到它的旋转方向，这是我们看到一个几何图形的第一印象．

其次，看看是什么旋转？因为旋转的种类有很多，你看它是点旋转还是线旋转或者是平面图形旋转·

最后，你再观察出有哪些三角形全等，从已知中找到两个三角形全等的条件（包括隐藏的对顶角、公共角、公共边等）．

只有掌握了这些信息，并以此为突破口，才能为解决此类问题奠定坚实的基础．

真题演练

选C