平行四边形——常用模型（一）平行线+中点

平行线+中点模型及变式经常会在平行四边形这一章进行运用，是必须要熟练掌握的方法，作为组合类辅助线，看见平行线+中点，还要想到延长法构造平行8字全等。下面让我们一起来研究下：

一、平行线+中点模型：

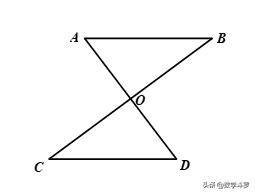
如图，AB∥CD，O是AD中点，则

O是BC中点.

易证：△AOB≌△DOC

二、平行线+中点变式：

如图，AB∥CD，AB=CD，则

O是AD中点,O是BC中点

同样，易证：△AOB≌△DOC

（平行线+中点得平行8字全等.）

三、此外，平行线+中点要想到延长法构造平行8字全等.

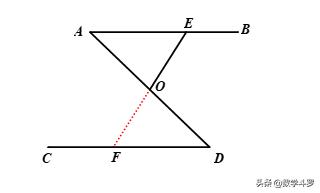
如图，AB∥CD，O为AD中点，E是AB上一点，

连接EO并延长交CD于点F，则O是EF中点.

结语：因为AB∥CD，所以∠A=∠D，∠B=∠C，又∠AOD=∠DOB，则△AOB与△COD的三对角都相等，要证明△AOB≌△DOC，只差一组对应边相等即可，简单说就是平行线+一组相等边就有全等三角形.

应用：

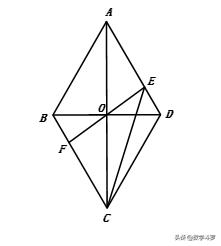
1. 已知，四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC，BD相交于点O，过点O的直线EF交AD于点E，交BC于点F.

（1）求证：△AOE≌△COF；

（2）若∠EOD=30°，求CE的长.

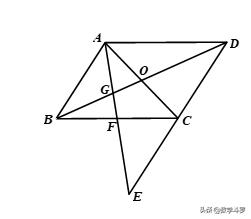
2. E为□ABCD中DC边的延长线上一点，且CE=DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于O，连接OF，判断AB与OF的位置关系和数量关系，并证明你的结论.