巧用替换法解决三角形的角度计算问题

三角形的角度计算问题是七年级数学的重要知识点，也是期末考试的必考点，本文就例题详细解析这类题型的解题思路，希望能给大家期末复习备考提供帮助。

例题1

在△ABC中，已知∠ABC=30°,点D在BC上，点E在AC上，∠BAD=∠EBC，AD交BE于F，

EG∥AD交BC于G，EH⊥BE交BC于H，求∠HEG的度数。

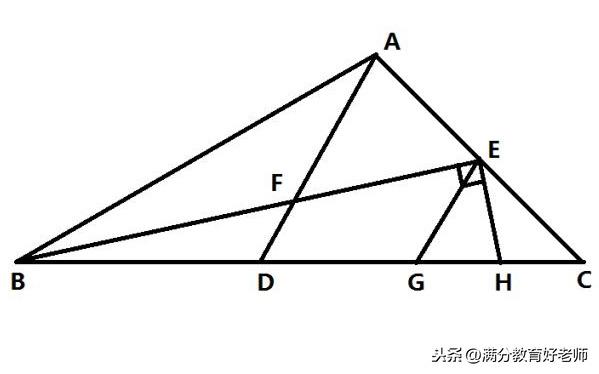
根据三角形的外角定理和题目中的条件：三角形的外角等于不相邻两个内角的和，∠BFD为△ABF的外角，则∠BFD=∠BAD+∠ABE。

根据题目中的条件和结论：∠BAD=∠EBC，∠BFD=∠BAD+∠ABE，∠ABC=∠EBC +∠ABE，则∠BFD=∠ABC。

根据题目中的条件：∠BFD=∠ABC，∠ABC=30°,则∠BFD=30°。

根据平行线的性质和题目中的条件：两直线平行同位角相等，EG∥AD，则∠BEG=∠BFD。

根据结论：∠BFD=30°，∠BEG=∠BFD，则∠BEG=30°。

根据题目中的条件：EH⊥BE，则∠BEH=90°。

根据题目中的条件：∠HEG=∠BEH-∠BEG，∠BEG=30°，∠BEH=90°，则∠HEG=60°。

例题2

如图，已知△ABC的两条高BD、CE交于点F，∠ABC的平分线与△ABC外角∠ACM的平分线交于点G，若∠BFC=8∠G，求∠A。

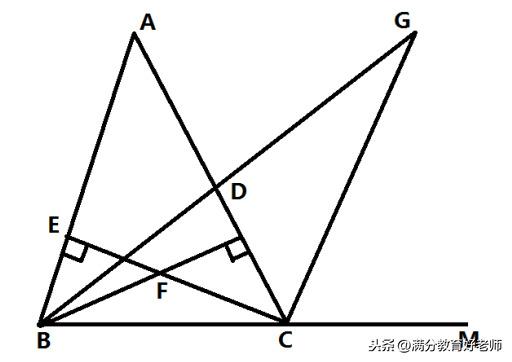
根据题目中的条件：BD、CE为△ABC的两条高，则BD⊥AC，CE⊥AB，即∠BDC=90°，∠CEB=90°。

根据题目中的条件和结论：∠BCD+∠CBD+∠BDC=180°，∠BCE+∠CBE+∠BEC=180°，∠BDC=90°，∠CEB=90°，则∠CBD+∠BCE=180°-(∠BCD+∠CBE)。

根据题目中的条件：∠A+∠BCD+∠CBE=180°,则∠BCD+∠CBE=180°-∠A。

根据结论：∠CBD+∠BCE=180°-(∠BCD+∠CBE)，∠BCD+∠CBE=180°-∠A，则∠CBD+∠BCE=∠A。

根据题目中的条件：∠BFC+∠CBD+∠BCE=180°，∠CBD+∠BCE=∠A，则∠BFC=180°-∠A。

根据三角形的外角定理和题目中的条件：三角形的外角等于不相邻两个内角的和，∠ACM是△ABC的外角，则∠ACM=∠A+∠EBC。

根据角平分线的性质，题目中的条件和结论：角平分线把一个角分成相等的两份，GC是∠ACM的平分线，∠ACM=∠A+∠EBC，则∠GCM=(∠A+∠EBC)/2。

根据角平分线的性质和题目中的条件：BG是∠ABC的平分线，则∠GBC=∠EBC/2。

根据三角形的外角定理、题目中的条件和结论：三角形的外角等于不相邻两个内角的和，∠GCM是△BGC的外角，则∠GCM=∠GBC+∠G。

根据结论：∠GCM=∠GBC+∠G，∠GBC=∠EBC/2，∠GCM=(∠A+∠EBC)/2，则∠G=∠GCM-∠GBC=∠A/2。

根据题目中的条件和结论：∠G=∠A/2，∠BFC=180°-∠A，∠BFC=8∠G，则∠A=36°。

结语

解决三角形的角度计算问题，需要灵活运用角平分线、外角和、平行线、垂直等相关的性质定理，才能得到相关角之间的数量关系进行计算。特别注意，对于无法直接计算的角度问题，需要借助替换法，用已知角的等式表示未知角或多个角的和，通过等式变换就能得到需要求解的值。