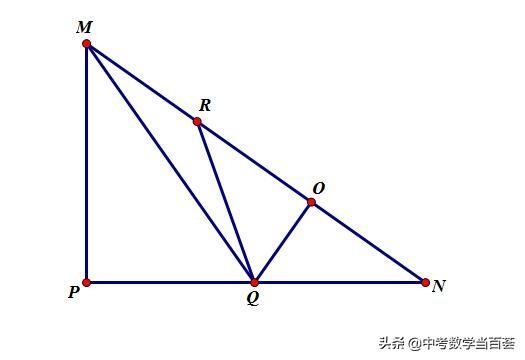
如图，在Rt△MPN中，∠P=90°，MP=6，NP=8，点Q为边NP上的一个动点（点Q不与点N重合），QO⊥MN，垂足为O，点R在边MN上，且与点N关于直线QO对称．

（1）求证△QON∽△MPN；

（2）若MQ平分∠PMN，求线段NQ的长；

（3）当△MRQ为等腰三角形时，求线段NQ的长．

分析

勾股定理求出MN=10

（1）略

（2）若MQ平分∠PMN时，则△PMQ与△OMQ全等，

在Rt△QON中，由勾股定理列出方程，解得QN

（3）当△MRQ为等腰三角形时，只有一种可能R为顶角（本题难点，为什么？），

此时，结合对称性得RM=RQ=NQ，RN=2NO，利用三角函数列方程求解的QN.

实际操作

（1）∠P=∠QON=90°，∠N=∠N

＝＞△QON∽△MPN

（2）由勾股定理得MN^2=6^2＋8^2=100

＝＞MN=10

MQ平分∠PMN时＝＞

∠PMQ=∠OMQ=90°，MQ=MQ ∠P=∠QON=90°

＝＞△PMQ≌△OMQ

＝＞OM=PM=6，OQ=PQ=x，QN=8－x，ON=4

在Rt△QON中，由勾股定理得（8－x）^2－x^2=4^2

＝＞x=3＝＞NQ=8－3=5

（3）N，R关于直线QO对称＝＞Rt△ONQ≌Rt△ORQ

＝＞∠N=∠QRN

在Rt△MPN中，∠P =90°

＝＞∠N＋∠PMN=90°

＝＞∠N为锐角

＝＞∠QRN为锐角

＝＞∠QRM为钝角

当△MRQ为等腰三角形时，

因为一个三角形中不可能有两个钝角

＝＞∠QRM必为顶角

＝＞RM=RQ=y

＝＞RQ=NQ=y，RN=2NO=10－y，PQ=OQ=8－y

cos∠N=ON：QN=PN：MN

＝＞（10－y）/2：y=8:10

＝＞8y=5（10－y）

＝＞y=50/13＝＞NQ=50/13

综述

（1）本题求线段NQ在不同时刻（角平分线、等腰三角形）的长度，利用方程思想来求解；

（2）列出方程的策略：勾股定理和三角函数（或相似三角形性质）

（3）问题（3）中，当△MRQ为等腰三角形时，要讨论孰腰孰底问题，利用对称性，得出只有一种可能R为顶角，不存在其他情况，这一细节是本题难点，必须详尽表达清楚。