试题再现

解答分析

做平面几何的题目，数形结合是一种很直观的方法。根据题目给出的条件我们做图，如图1 ：

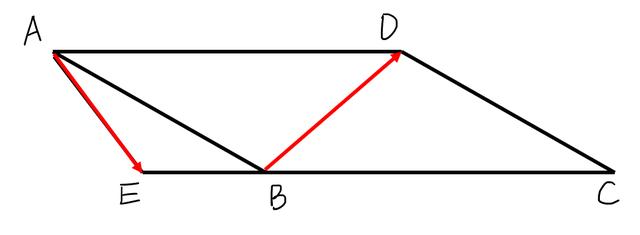
图1

不管是用基底法还是坐标法，我们都需要求出各边、角的大小关系：

【方法一：基底法】

本题中，从题中可以得知AB、AD的长度以及角A的大小，故而选取向量AB和向量AD作为基底，用基底表示向量AE和向量BE，然后在进行计算：

答题套路：

1. 选基底：根据已知条件，选择合适基底，将所求的平面向量的数量积转化为易求的平面向量的数量积运算；

2. 转化：利用数量积的定义：a点乘b=|a||b|cos θ 以及 a 点乘 a = (|a|)^2 ，将平面向量数量积运算转化为一般的运算；

3. 求数量积 ：将已知条件代入求解即可。

4. 基底法的关键是选好基底。

使用基底法还需注意两点：一是两向量的夹角，这是常常出现问题的地方；而是注意区分数量积的运算性质与向量的数乘、实数与实数之积之间的差异。

【方法二：坐标法】

坐标法，顾名思义就是利用坐标来求解平面向量数量积的。

首先构建如图2坐标系：

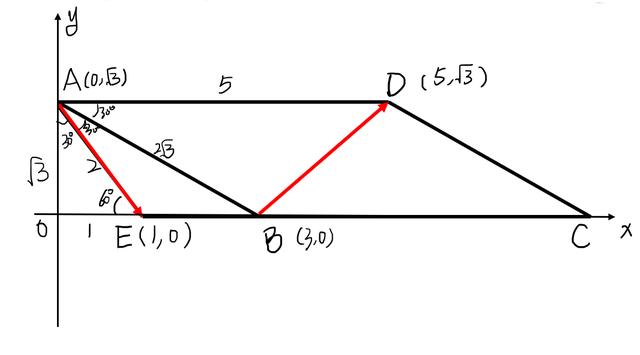
图2

求出各点坐标，进而求出向量进行计算即可:

答题套路：

1. 建系：根据已知条件，建立恰当的直角坐标系，并求出各点坐标；

2. 求向量：利用向量坐标公式求出所需向量。

3. 求数量积：根据平面向量数量积公式 a 点乘 b = x1x2+y1y2 ，计算向量数量积。

使用坐标法的关键在与准确的求出向量的坐标，是终点的坐标减去起点的坐标。

高考真题测试

看完这篇文章，相信同学们都有一定的收获，想要实际应用一下所学是否扎实的同学可以做一下下面这道题，这是2018年天津卷第8题，两种方法都可以尝试一下。

选A