八年级物理难题解析：浮力比值问题

例题

一个竖直放置在水平桌面上的圆柱形容器，内装密度为ρ的液体。将挂在弹簧测力计下的金属块A浸没在该液体中（A与容器底未接触），金属块A静止时，弹簧测力计的示数为F1；将木块B放入该液体中，静止后木块B露出液面的体积与其总体积之比为7:10；将挂在弹簧测力计下的金属块A放在B上面，使木块B刚好浸没入液体中，如图所示，弹簧测力计的示数为F2。若已知金属块A的体积与木块B的体积之比为13:20，求金属块A的体积。

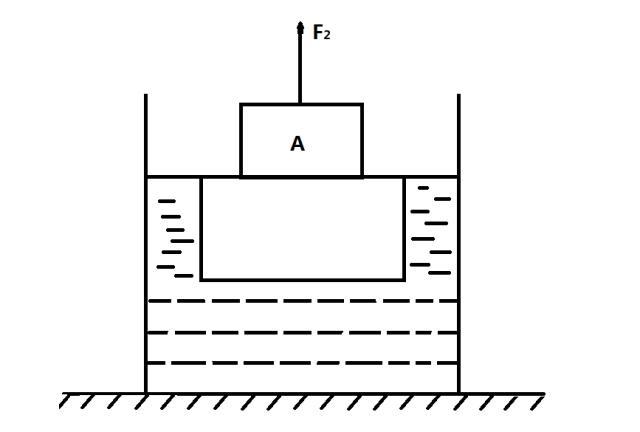
1、金属块A浸没在液体中

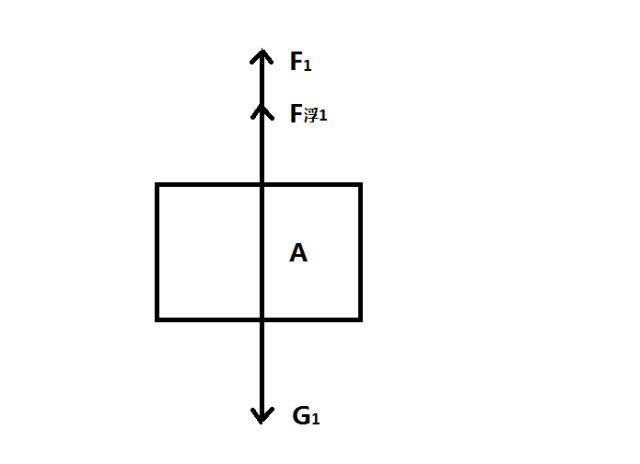
对金属块A进行受力分析，在竖直方向上受到竖直向下的重力G1，竖直向上的浮力F浮1和弹簧测力计的拉力F1；

根据物体受力平衡的条件：金属块A静止，处于平衡状态，则竖直方向上受力和为零，即G1= F浮1+ F1；

根据浮力的计算公式和题目中的条件：F浮1=ρ液gV排1，ρ液=ρ，V排1=V1，则F浮1=ρgV1；

根据重力的计算公式、题目中的条件和结论：G1=ρ1gV1，F浮1=ρgV1，G1= F浮1+ F1，则F1=ρ1gV1-ρgV1=(ρ1-ρ)gV1，即ρ1=F1/ gV1+ρ。

2、木块B放入液体中

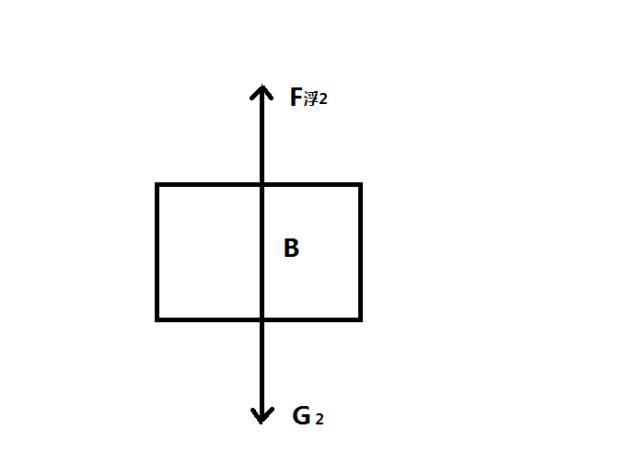
对木块B进行受力分析，在竖直方向上受到竖直向下的重力G2和竖直向上的浮力F浮2。

根据物体受力平衡的条件：木块B静止，处于平衡状态，则竖直方向上受力和为零，即G2= F浮2。

根据题目中的条件：木块B露出液面的体积与其总体积之比为7:10，则V排2=3/10V2。

根据浮力的计算公式、题目中的条件和结论：F浮2=ρ液gV排2，ρ液=ρ，V排2=3/10V2，则F浮2=3/10ρgV2。

根据重力的计算公式、题目中的条件和结论：G2=ρ2gV2，F浮2=3/10ρgV2，G2= F浮2，则ρ2gV2=3/10ρgV2，即ρ2=3/10ρ。

3、金属块A放在木块B的上面

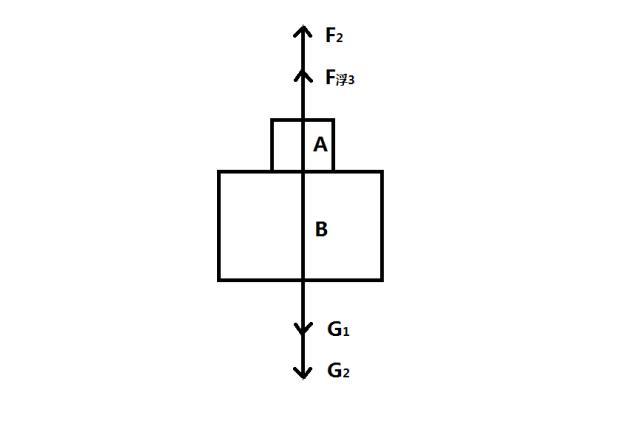
把金属块A和木块B作为一个整体进行受力分析，在竖直方向上受到竖直向下的重力和(G1+G2)，竖直向上的浮力F浮3和弹簧测力计的拉力F2。

根据物体受力平衡的条件：金属块A和木块B静止，处于平衡状态，则在竖直方向上受力和为零，即G1+G2= F浮3+ F2。

根据浮力的计算公式、题目中的条件和结论：F浮3=ρ液gV排3，ρ液=ρ，V排3=V2，则F浮3=ρgV2。

根据结论：G1=ρ1gV1，G2=ρ2gV2，F浮3=ρgV2，G1+G2= F浮3+ F2，

则F2=ρ1gV1+ ρ2gV2-ρgV2。

根据题目中的条件和结论：V1：V2=13:20，F2=ρ1gV1+ ρ2gV2-ρgV2，

则F2=(ρ1+20/13ρ2-20/13ρ)gV1。

根据结论：ρ1=F1/ gV1+ρ，ρ2=3/10ρ，F2=(ρ1+20/13ρ2-20/13ρ)gV1，

则V1=13(F1-F2)/ ρg。

结语

浮力中的比值问题的难度在于题目中给出的已知条件以比值居多，可以直接利用的物理量较少，需要同学们认真分析，将这些比值转换为可以利用的有用条件，因此这里题型的解题思路如下：

认真审题，找准受力分析对象，逐一画出全面具体的受力图；

利用平衡条件，得到每个受力分析对象所受各个力之间的数量关系；

利用力学计算公式和题目中的比值条件，对公式进行变换，得到其他相关物理量之间的比值关系；

综合各个受力分析对象得到的比值关系，根据题意进行最后的汇总计算，得到需要求解的物理量的值。