中考必考知识点：二次函数8个例题简要分析

今天我们就以下8个例题简单分析一下二次函数几个重要考点。

【例题1】

【分析】

（1）确定顶点坐标和与x轴y轴交点，作出图形；

（2）方程x2﹣2x﹣1＝0的根就是二次函数y＝x2﹣2x﹣1的函数值为0时的横坐标x的值；

（3）观察图象可知图象与x轴交点的横坐标即为方程的根．

【解答】

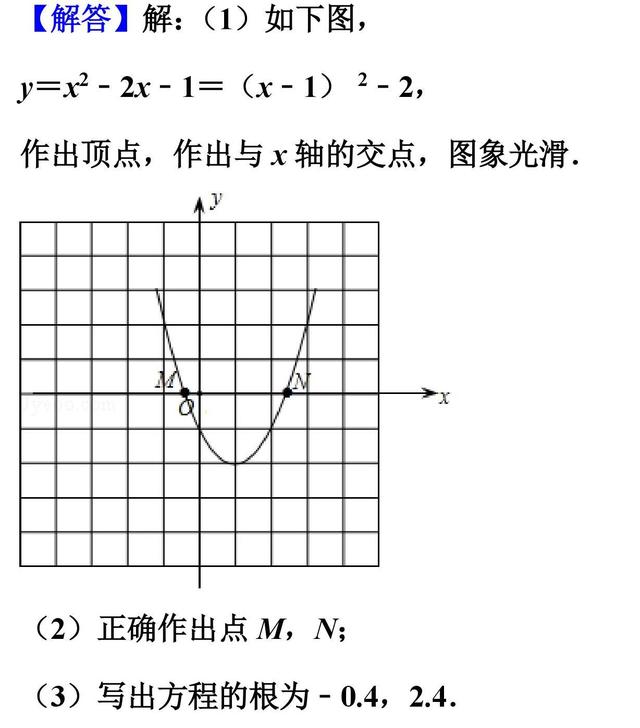
【点评】本题考查了图象法求一元二次方程的近似值，二次函数与一元二次方程的关系，解答此题的关键是求出对称轴，然后由图象解答，锻炼了学生数形结合思想的运用．

【例题2】

【分析】

（1）根据二次项的系数等于零，一次项的系数不等于零，可得方程组，根据解方程组，可得答案；

（2）根据二次项的系数不等于零，可得方程，根据解方程，可得答案．

【解答】

【点评】本题考查了二次函数的定义，二次函数的二次项的系数不等于零是解题关键．

【例题3】

【分析】

（1）抛物线的顶点D的横坐标是2，则x＝﹣＝2，抛物线过是A（0，﹣3），则：函数的表达式为：y＝ax2+bx﹣3，把B点坐标代入函数表达式，即可求解；

（2）分AB＝AC、AB＝BC、AC＝BC，三种情况求解即可；

（3）由S△PAB＝•PH•xB，即可求解．

【解答】

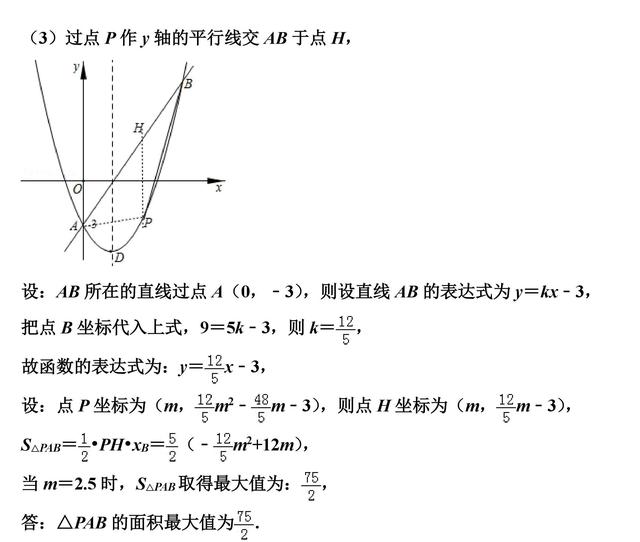
【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．

【例题4】

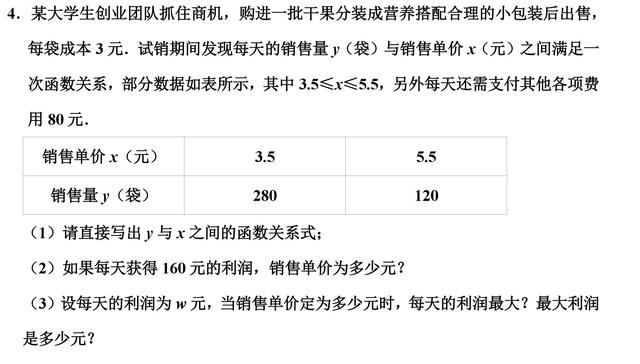
【分析】

（1）根据每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，可设y＝kx+b，再将x＝3.5，y＝280；x＝5.5，y＝120代入，利用待定系数法即可求解；

（2）根据每天获得160元的利润列出方程（x﹣3）（﹣80x+560）﹣80＝160，解方程并结合3.5≤x≤5.5即可求解；

（3）根据每天的利润＝每天每袋的利润×销售量﹣每天还需支付的其他费用，列出w关于x的函数解析式，再根据二次函数的性质即可求解．

【解答】

【点评】本题考查了二次函数的应用，一元二次方程的应用，待定系数法求一次函数的解析式，根据题意找出等量关系列出关系式是解题的关键．

【例题5】

【分析】

（1）根据函数的图象过（1，0）（0，3），再代入y＝﹣x2+bx+c，列出方程组，即可求出b，c的值；

（2）把函数化为顶点式，求得对称轴和最大值即可．

【解答】

【点评】此题考查了用待定系数法求二次函数的解析式，以及识图能力，即将求解的问题转化为图象上隐含的某个信息．

【例题6】

【分析】当k分别取﹣1，1，2时，函数y＝（k﹣1）x2﹣4x+5﹣k表示不同类型的函数，需要分类讨论，最终确定函数的最值．

【解答】

【点评】本题考查了二次函数的最值．需要根据k的不同取值进行分类讨论，这是容易失分的地方．

【例题7】

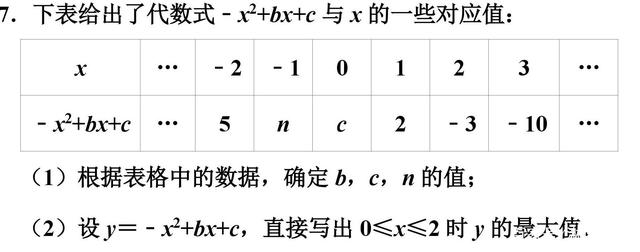
【分析】

（1）把（﹣2，5）、（1，2）分别代入﹣x2+bx+c中得到关于b、c的方程组，然后解方程组即可得到b、c的值；然后计算x＝﹣1时的代数式的值即可得到n的值；

（2）利用表中数据求解．

【解答】

【点评】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．

【例题8】

【分析】

（1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式；

（2）利用（1）的解析式求该二次函数图象的对称轴和顶点坐标；

（3）根据二次函数的图象的单调性解答．

【解答】

【点评】此题主要考查了二次函数顶点坐标的求法，二次函数图象的性质．二次函数的解析式有三种形式：

（1）一般式：y＝ax2+bx+c（a≠0，a、b、c为常数）；

（2）顶点式：y＝a（x﹣h）2+k；

（3）交点式（与x轴）：y＝a（x﹣x1）（x﹣x2）．