人教版八年级下学期——直角三角形斜边上的中线及其变式拓展
直角三角形斜边上的中线性质,作为直角三角形的一个很重要的性质定理,平时大家都做过很多类似的题型,普遍掌握的还可以,但是变式拓展类,却不尽如人意,很多同学拿到题没有思路,或者有思路(似曾相识),过程又不会书写,导致考试时效率低下。针对这种情况,下面我们从最基础的结论开始入手,先证明,然后应用。
直角三角形斜边上的中线性质:直角三角形斜边上的中线等于斜边的一半.

直角三角形斜边上的中线将其分成了两个等腰三角形.(一直角得两等腰)
接下来,我们重点研究下与直角三角形斜边上的中线有关的变式:
变式1:

如果三角形一条边上的中线等于这条边的一半,则这个三角形是直角三角形.
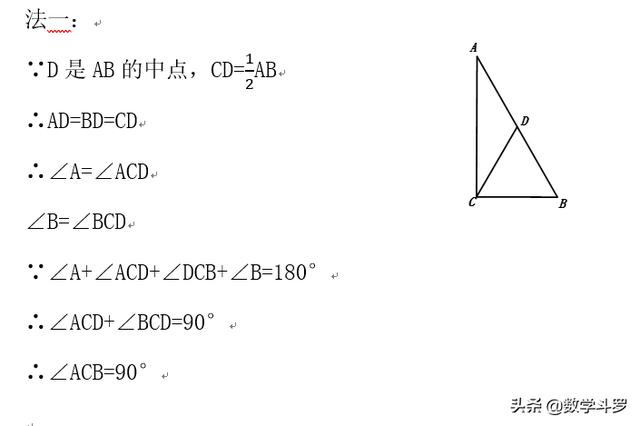
两等腰得一直角

变式2:

一直角一等腰得一等腰
(将条件改成CD=BD,同理可证!)
结语:上述结论的证明利用了我们学过的倍长中线法、等腰三角形的性质和判定,矩形的性质和判定等,变式1和2在大题中不可直接作为结论来用,因此要在平时养成习惯,模块化过程,提高做题效率。
应用:
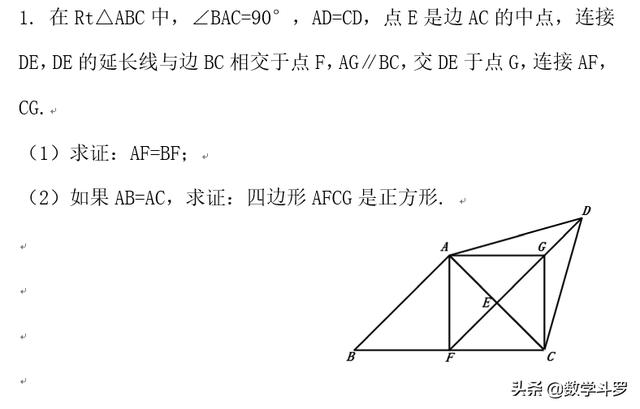
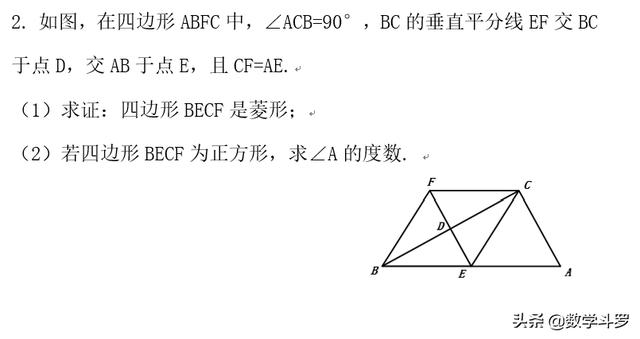

 加载中,请稍侯......
加载中,请稍侯......
精彩评论