扬州中考数学，学生考后比较轻松，27题几何代数相结合

扬州中考数学的第27题看起来是一道几何题，实际考的知识点是二次函数的最值。

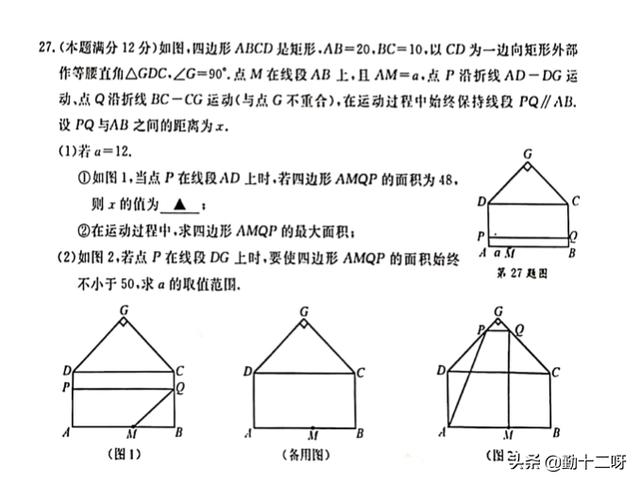
第（1）小问不是很难，已知四边形AMQP的面积，要求x的值，也就是知道求梯形的高，直接利用梯形的面积公式求解即可。

第（2）小问求的是四边形AMQP面积的最大值。在运动的过程中，点P可能在线段AD上，也可能在线段DG上面，因此要分两种情况进行讨论。分别是0≤x≤10和10＜x≤20，然后在两个范围内分别求出最大值再比较大小。可以发现，当0≤x≤10时，面积是一个一次函数，在x=10时取得最大值，而当10＜x≤20时，面积是关于x的二次函数，一个开口向下的二次函数，通过求解可以发现在对称轴直线x=13处取得最大值。将两个最大值比较大小，最终可以得到答案。

这两小问相对来说难度不大，只要基本功扎实应该难不倒考生。

其实，只要第（2）小问有思路，最后一小问的表达式应该可以表达出来。最后一小问，明确告诉我们，点P在线段DG上，换言之，只存在一种情况，就是10≤x≤20。和第（2）小问表达式一样，只不过多了一个参数a，也就是把第（2）问中的下底12变成a。这道题目的关键就是怎么处理最值问题，这是一个开口向下的二次函数，而题目中要求的是面积始终不小于50，我们应该去求最小值。本来应该要分两种情况讨论，两个端点处都可能取得最小值，但是可以发现二次函数的对称轴比15小，因此只能在x=20处取得最小值。

开口向下的二次函数，自变量离对称轴越近，函数值越大，自变量离对称轴越远，函数值越小；开口向上的二次函数，自变量离对称轴越近，函数值越小，自变量离对称轴越远，函数值越大。

总体来说，这道题目的难度不是很大，但是学生平时做题目习惯性地在二次函数的对称轴处取得最大值和最小值，会造成一定的影响，希望考生们在考场里能冷静发挥。