94.如图1，MN为⊙O的直径，弦PQ⊥MN于T，R为MN延长线上一点，PR交⊙O于点S .

（1）求证：NS平分∠QSR；

（2）若SQ=SR，NR=5，MT= 9/4，求⊙O的半径．

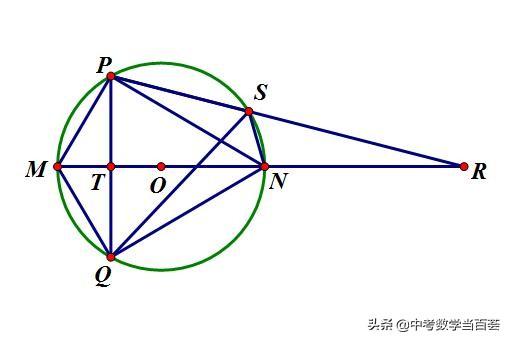
图1

分析

（1）利用垂径定理，证明MN垂直平分PQ，再利用圆内接四边形、等边对等角、同弧上圆周角相等，即可得证；

（2）在Rt△MPN中，利用射影定理列方程，求解。

实际操作

（1）MN为⊙O的直径，弦PQ⊥MN＝＞T为PQ中点

＝＞MN是PQ中垂线＝＞NP=NQ

＝＞∠NQP=∠NPQ =∠NSQ

⊙O内接四边形NSPQ＝＞∠RSN=∠NQP

∴∠NSQ=∠RSN 即NS平分∠QSR

（2）SQ=SR ∠NSQ=∠RSN SN=SN

＝＞△SQN≌△SRN＝＞NQ=NR=NP=5

MN为⊙O的直径＝＞∠MPN=90°且PQ⊥MN

＝＞PN^2=TN×NM=(MN－MT) ×NM

＝＞25=(MN－9/4) ×MN

＝＞MN=25/4＝＞⊙O的半径=25/8

综述

本题虽然为中档题，难度一般，但涉及10多个知识点，需要较扎实的基本功。

主要知识点：垂径定理，中垂线性质，弦等角等（或等边对等角），直径所对圆周角=90°，圆内接四边形性质，全等三角形判定及性质，相似三角形（射影定理或三角函数），解一元二次方程。