破解二次函数参数难题的图解策略

二次函数是初中数学的核心内容，也是重要的基础知识和重要的数学思想方法，它是其他所有与数量关系相关问题的思想基础和知识基础，诸如众多的二次方程问题，不等式问题，几何图形中的几何量的关系问题（特别是与运动相关的几何图形问题），或隐或显地都以二次函数作为指引、依据和基础。尤其二次函数的参数问题，更需充分发掘二次函数图像特征，利用数形结合破解这类考试高频考试题型，以形助数,使数量关系和几何图形巧妙地结合起来，使问题得以解决。

1. （2019•安徽中考数学）在平面直角坐标系中，垂直于x轴直线l分别与函数y=x-a+1和y=x²-2ax的图象相交于点P,Q两点，若平移直线l,可以使P，Q都在x轴下方，则实数a的取值范围是_____

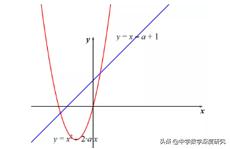
解析：直线l的平移，也就是x在某个范围时，两个函数都小于0，由于一次函数中k>0,二次函数中a>0，所以要使两个函数同时存在小于0的值，即两函数交点中较小的值应小于0

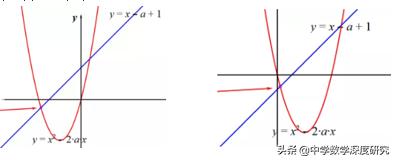
联立解析式求交点，计算量较大，不妨我们取特殊值，如令此交点位于x轴上，如下图

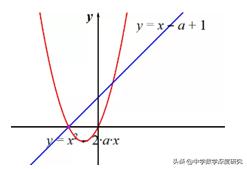
即：y=x-a+1==x²-2ax=0，解得a=±1

根据函数图象的平移，可得a的取值为a>1或a<-1

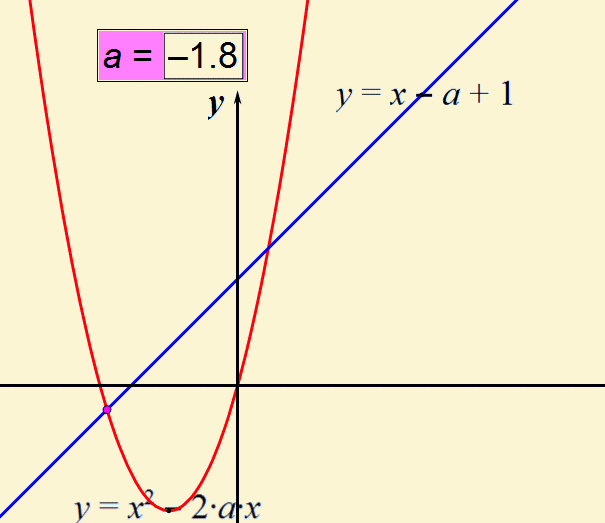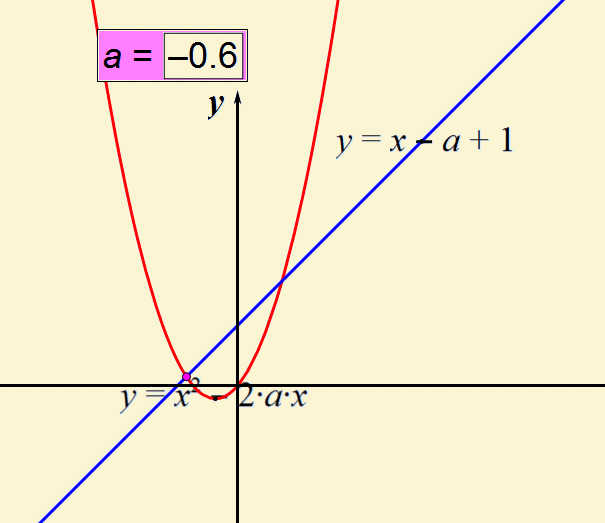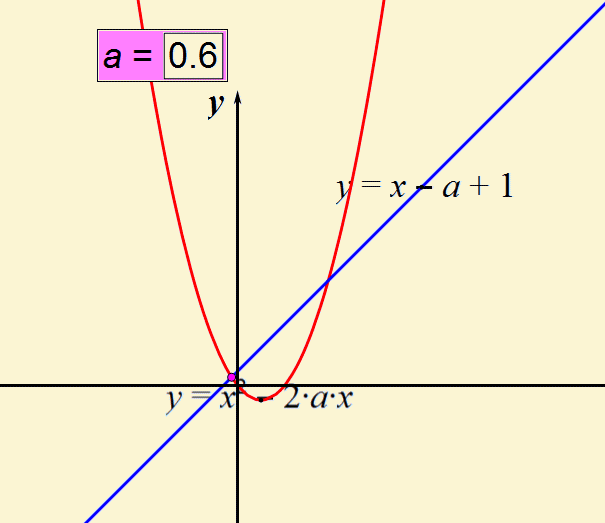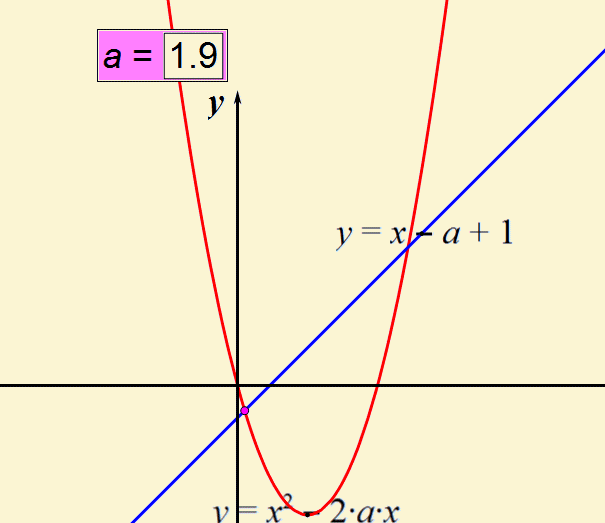
说明：本题是今天上午刚考过的安徽中考题，很多同学对这道感到很难，如果借助下面动态演示，我们很容易求解这一问题。

2．（2019•蕲春县模拟）如图，抛物线y＝﹣2x²﹣8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C₁问左平移得C₂，C₂与x轴交于点B，D．若直线y＝﹣x+m与C₁，C₂共有3个不同的交点，则m的取值范围是 ______．

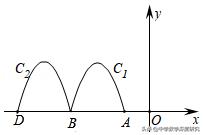
【分析】本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识，解答本题的关键是正确地画出图形，利用数形结合进行解题，此题有一定的难度．首先求出点A和点B的坐标，然后求出C₂解析式，分别求出直线y＝x+m与抛物线C₂相切时m的值以及直线y＝x+m过点B时m的值，结合图形即可得到答案．

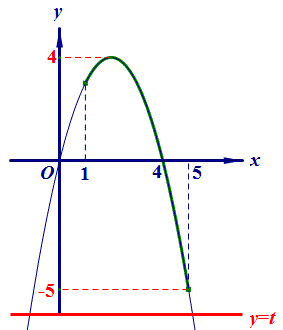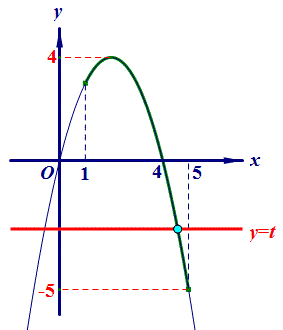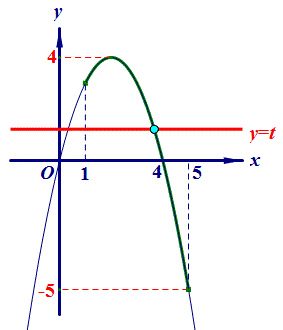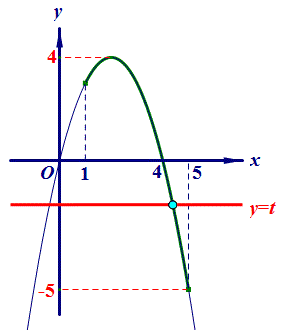
3.（2019•邯郸模拟）二次函数y＝﹣x²+mx的图象如图，对称轴为直线x＝2，若关于x的一元二次方程﹣x²+mx﹣t＝0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）

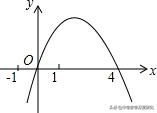
A．t＞﹣5B．﹣5＜t＜3C．3＜t≤4D．﹣5＜t≤4

【分析】如图，关于x的一元二次方程﹣x²+mx﹣t＝0的解就是抛物线y＝﹣x2+mx与直线y＝t的交点的横坐标，利用图象法即可解决问题．

【解答】如图，关于x的一元二次方程﹣x²+mx﹣t＝0的解就是抛物线y＝﹣x²+mx与直线y＝t的交点的横坐标，

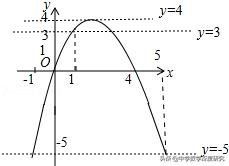
当x＝1时，y＝3，当x＝5时，y＝﹣5，

由图象可知关于x的一元二次方程﹣x²+mx﹣t＝0（t为实数）在1＜x＜5的范围内有解，直线y＝t在直线y＝﹣5和直线y＝4之间包括直线y＝4，∴﹣5＜t≤4．故选：D．

本题采用如下动态演示更容易确定问题答案。

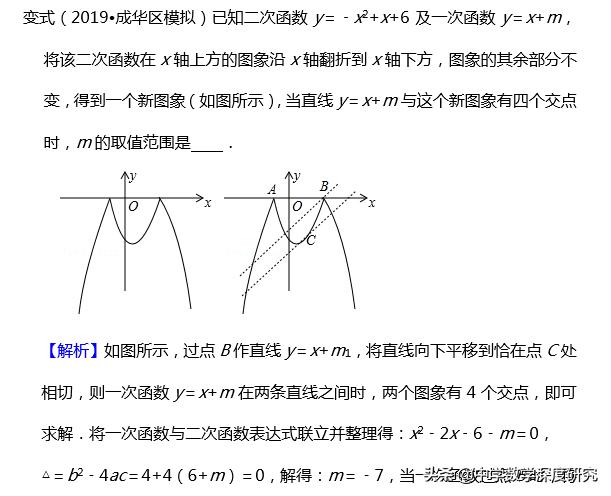
点B坐标代入：y＝x+m得：0＝3+m，解得：m＝﹣3，故答案为：﹣7＜m＜﹣3．

总结：这是在函数类型题目中比较常见。解题时，要细心冷静地分析出符合条件的所有可能性，然后数形结合去求解，去判断确定，应注意解题要精准明确数学问题的条件和结论之间的内在联系，既分析其代数意义，又揭示其几何直观，使数量关系的精确刻划与几何图形的直观形象巧妙、和谐地结合在一起，充分利用这种结合，寻找解题思路，使问题化难为易、化繁为简，从而得到解决。