试题再现

分析

先设点P(t,0),A(x1,y1),B(x2,y2)

（1）根据韦达定理以及抛物线定义，可求得直线l的方程。

（2）由向量关系得到t-x1=3(x2-t)，结合韦达定理求得t、x1、x2的值，利用弦长定理可得|AB|的值。

解答

在求解抛物线弦长问题时，先设点坐标，写出直线方程，再将其代入抛物线方程中，根据题目需要消去x或y，得到关于y或x的一元二次方程，这个方程必有两根，这时可以利用韦达定理求出两根的和及乘积，以供后续使用。

韦达定理

（1）

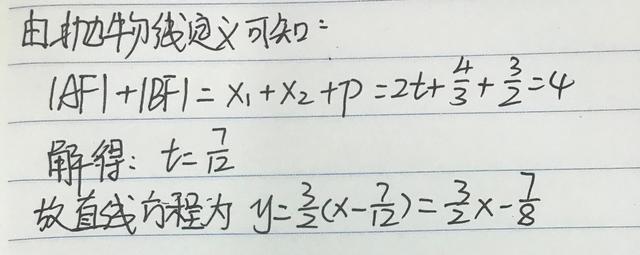
抛物线是指平面内到一个定点F（焦点）和一条定直线l（准线）距离相等的点的轨迹。

当抛物线开口向右时，有|AF|+|BF|=x1+x2+p：

|AF|+|BF|=x1+x2+p

同理：

当抛物线开口向左时，有|AF|+|BF|=-x1-x2+p；

当抛物线开口向上时，有|AF|+|BF|=y1+y2+p；

当抛物线开口向右时，有|AF|+|BF|=-y1-y2+p。

(2)

已知直线的斜率，以及弦|AB|两端点的横坐标或纵坐标，求弦长时，最快方式是使用弦长公式。

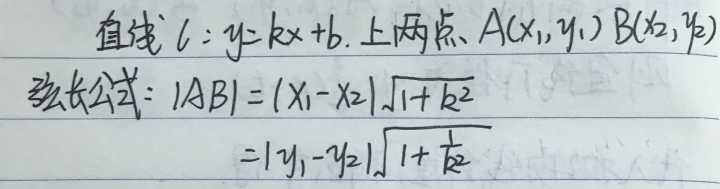
弦长公式

该公式由两点间距离公式推导而来：

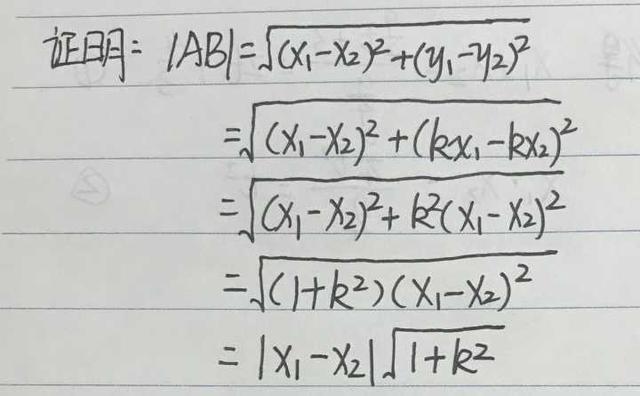
弦长公式不仅可在抛物线弦长问题中使用，任何时候，只要知道线段两端点横坐标/纵坐标以及斜率时均可使用，也算是万能公式了。