二次函数综合大题

例题.

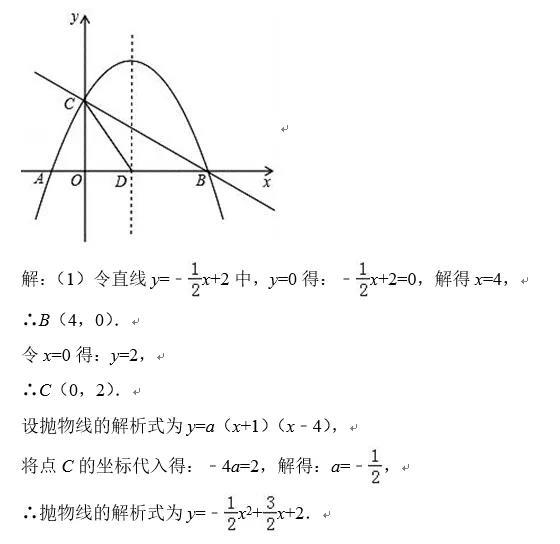
如图，直线y=﹣x/2+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点A（﹣1，0）．

（1）求该二次函数的关系式；

（2）若抛物线的对称轴与x轴的交点为点D，则在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；

（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

考点分析：

二次函数综合题．

题干分析：

（1）先求得B、C的坐标，然后设抛物线的解析式为y=a（x+1）（x﹣4），将点C的坐标代入求解即可；

（2）如图1所示：先求得抛物线的对称轴方程则可得到OD的长，然后依据勾股定理可求得CD的长，然后可求得点P和点P′的坐标，然后过点C作CE⊥对称轴，垂足为E，然后依据等腰三角形的性质可得到DE=OC=2，故此可得到点P″的坐标；

（3）设点F（a，﹣a2/2+3a/+2），则E（a，﹣a/2+2），则FE=﹣a2/2+2a，然后可得到△CBF的面积与a的函数关系式，从而可得到△CBF的最大值，从而可确定出点E的坐标，最后依据四边形CDBF的最大面积=△CBD的面积+△BCF的最大面积求解即可．

第三小题涉及的知识点依旧是铅锤法的运用，用各地模拟题来看，铅锤法的题目出现的频率还是较高的，所以同学们要多注意。