一题多解系列02——旋转的45°角

题：如图1，正方形ABCD中，E、F分别是BC、CD上的点，∠EAF=45°，求EF/AB的最小值.

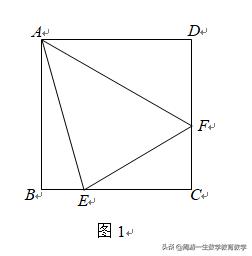
此题难度一般，本人在《经典再现22》一文中抛出了一块砖(如下解法一)，引来了多块玉，许多网友纷纷评论，给出了更为巧妙简便的解法，现整理为如下的解法二、三、四。或许还有其他解法，欢迎各位高手不吝赐教。

解法一：如图2，连接AC.则∠BAC=∠DAC=45°，

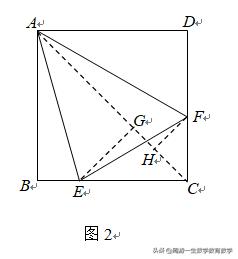
所以∠BAE+∠EAC=45°，

因为∠EAF=45°，

所以∠EAC+∠CAF=45°，

所以∠BAE=∠CAF.

同理，∠DAF=∠CAE.

作EG⊥AC于G，FH⊥AC于H，则

∠AGE=∠AHF=∠B=∠D=90°，

所以△ABE∽△AHF，△ADF∽△AGE，

所以BE/HF=AE/AF，DF/GE=AF/AE，

两式相乘，得

BE/HF•DF/GE= AE/AF•AF/AE=1，

所以BE•DF=GE•HF，

因为△GCE和△HCF都是等腰直角三角形，

所以GE=CE/√2，HF=CF/√2，

所以BE•DF=CE•CF/2.

设正方形ABCD的边长为1，CE=x，CF=y，则

BE=1-x，DF=1-y，

所以(1-x)(1-y)=xy/2，

整理，得xy=2(x+y)-2，

所以EF=√(x^2+y^2)

=√[(x+y)^2-2xy]

=√[(x+y)^2-4(x+y)+4]

=√[(x+y)-2]^2

=|x+y-2|，

显然，x+y<2，

所以EF=2-(x+y).

设x+y=s，则EF=2-s，y=s-x，

因为xy=2(x+y)-2，

所以xy=2s-2，

所以x(s-x)=2s-2，

整理，得x^2-sx+2s-2=0，

因为x为实数，

所以△=s^2-4(2s-2)≥0，

即s^2-8s+8≥0，

解得s≥4+2√2或s≤4-2√2，

所以s最大值为4-2√2，

所以EF最小值=2-(4-2√2)=2√2-√2.

所以EF/AB的最小值为2√2-2.

解法二：如图3，因为四边形ABCD为正方形，

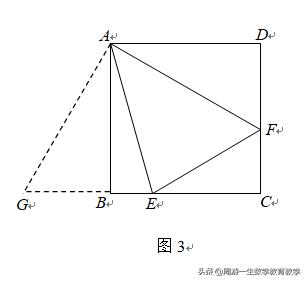
所以AB=AD，∠DAB=90°，

所以将△ADF绕点A顺时针旋转90°，得△ABG，则

AG=AF，BG=DF，∠BAG=DAF，∠ABG=∠D=90°，

所以G、B、E三点共线，

所以EG=BG+BE=DF+BE。

在△AGE 与△AEF中，

因为∠EAF=45°，

所以∠BAE+∠DAF=45°，

所以∠GAE=45°=∠EAF，

又AE=AE，

所以△AGE≌△AEF，

所以EF=EG，

设正方形ABCD的边长为1，BE=a，DF=b，则

EF=a+b，CE=1-a，CF=1-b，

在Rt△CEF中，由勾股定理，得

(1-a)^2+(1-b)^2=(a+b)^2，

整理，ab+a+b-1=0，

设a+b=s，则a=s-b，代入上式，得

(s-b)b+s-b+b-1=0，

整理，得b^2-sb+1-s=0，

因为b为实数，

所以△=s^2-4(1-s)≥0，

即s^2+4s-4≥0，

解得s≥-2+2√2，或s≤-2-2√2(舍去)，

所以s最小值为2√2-2，

即EF的最小值为2√2-2.

所以EF/AB的最小值为2√2-2.

解法三：如图1，设正方形ABCD的边长为1，BE=a，DF=b，则CE=1-a，CF=1-b，

在△EAF和△CEF中，分别由余弦定理和勾股定理，得

AE^2+AF^2-2AE•AF•cos∠EAF= EF^2=CE^2+CF^2，

即1+a^2+1+b^2-2√(1+a^2)• √(1+b^2)cos45°=(1-a)^2+(1-b)2，

整理，得

2(a+b)= √2•√(1+a^2)• √(1+b^2)，

两边平方，整理，得'

a^2+b^2+4ab=1+ a^2b^2，

再整理，得

a^2+b^2+2ab=1-2ab+ a^2b^2，

即(a+b)^2=(1-ab)2，

因为a+b>0，ab<1，

所以a+b=1-ab，

设a+b=s，则仿照解法二，得

s最小值为2√2-2。

又EF^2=(1-a)^2+(1-b)2

=2-2(a+b)+a^2+b^2，

=2-2(1-ab)+ a^2+b^2

=2ab+a^2+b^2

=(a+b)^2，

所以EF=a+b，

所以EF最小值为2√2-2，

所以EF/AB最小值为2√2-2。

解法四：设正方形ABCD的边长为1，BE=a，DF=b，∠BAE=α，则

∠DAF=45°-α，tanα=a，tan(45°-α)=b，

又tan(45°-α)=

(tan45°+tanα)/(1+tan45°•tanα)

=(1-a)/(1+a)，

所以(1-a)/(1+a)=b，

在Rt△CEF中，

CE=1-a，

CF=1-b=1-(1-a)/(1+a)=2a/(1+a)，

所以EF=√(CE^2+CF^2)

=√[(1-a)^2+4a^2/(1+a)^2]

=√[(1-a)^2(1+a)^2+4a^2]/(1+a)

=√(1+2a^2+a^4)/(1+a)

=√(1+a^2)^2/(1+a)

=(1+a^2)/(1+a)，

设EF=s，则s=(1+a^2)/(1+a)，

去分母，得s+sa=1+a^2，

整理为关于a的一元二次方程，得

a^2-sa+1-s=0，

因为a为实数，

所以△=s^2-4(1-s)≥0，

即s^2+4s-4≥0，

解得s≥-2+2√2，或s≤-2-2√2(舍去)，

所以s最小值为2√2-2，

即EF的最小值为2√2-2.

所以EF/AB的最小值为2√2-2.