知识要点

鸟头模型，又称共角模型。在两个三角形中，有一个角相等或互补，这两个三角形叫作共角三角形。共角模型常见图形，如图所示。

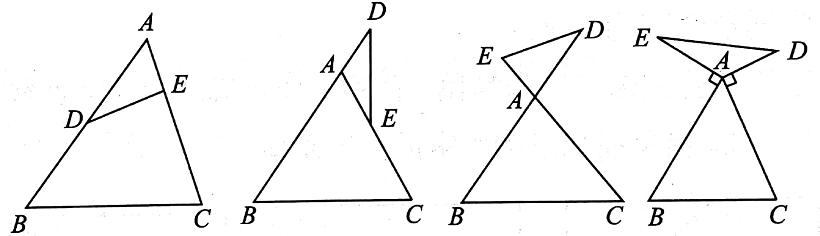
在这样的图形中，

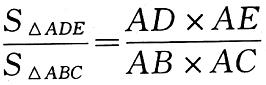
也就是说，共角三角形的面积比等于对应角（相等角或互补角）两夹边的乘积之比。

精选例题

如图，已知△ABC的面积为1，延长AB至点D，使BD=AB，延长BC至点E，使CE=2BC，延长CA至点F，使AF=3AC。求三角形DEF的面积。

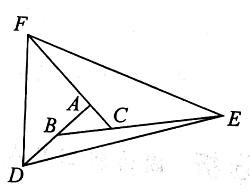
分析解答

已知△ABC和△BDE、△ADF、△CEF都分别组成了鸟头模型，那么知道线段的比例关系，就可用鸟头模型求解。

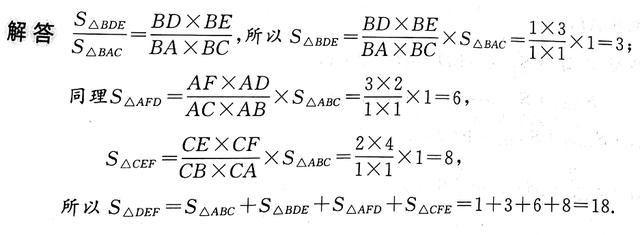
方法二：等高模型

分析：

连接AE和CD，要求三角形DEF的面积，可以分成三部分（△FCD+△FCE+△DCE）来分别计算，三角形ABC是一个重要的条件，抓住图形中与它同高的三角形进行分析计算，即可解得下面大三角形的面积．

解答：

接AE和CD，如图

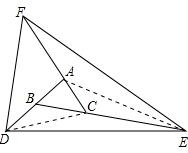
∵BD=AB，

∴S△ABC=S△BCD=1,S△ACD=1+1=2，

∵AF=3AC，

∴FC=4AC，

∴S△FCD=4S△ACD=4×2=8，

同理可以求得：S△ACE=2S△ABC=2,则S△FCE=4S△ACE=4×2=8；

S△DCE=2S△BCD=2×1=2；

∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18.