全等三角形的判定和性质是七年级数学的重要知识点，也是初中几何的入门，很多同学在学习过程中感觉比较费解，本文就例题详细讲解知识点及几何证明题的解题思路，希望能给同学们的复习备考提供帮助。

例题

如图1，已知正方形ABCD（正方形四条边都相等，四个角都是直角），把一个直角与正方形叠合，使直角顶点与一重合，当直角的一边与BC相交于E点，另一边与CD的延长线相交于F点时。

（1）证明：BE＝DF；

（2）如图2，作∠EAF的平分线交CD于G点，连接EG。证明：BE＋DG＝EG；

（3）如图3，将图1中的“直角”改为“∠EAF＝45°”，当∠EAF的一边与BC的延长线相交于E点，另一边与CD的延长线相交于F点，连接EF。线段BE，DF和EF之间有怎样的数量关系？并加以证明。

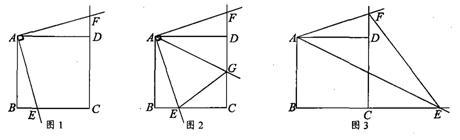
1、证明：BE＝DF

根据题目中的条件：正方形的四个角都为直角，则∠DAB=90°，∠B=90°，∠ADC=90°；

根据题目中的条件和结论：∠DAB=90°，∠DAB=∠BAE+∠DAE，则∠BAE+∠DAE=90°；

根据题目中的条件：∠EAF=90°，∠EAF =∠DAF+∠DAE，则∠DAF+∠DAE=90°；

根据结论：∠BAE+∠DAE=90°，∠DAF+∠DAE=90°，则∠BAE=∠DAF；

根据题目中的条件和结论：∠ADC=90°，∠ADF+∠ADC=180°，则∠ADF=90°；

根据结论：∠ADF=90°，∠B=90°，则∠B=∠ADF；

根据题目中的条件：正方形的四条边都相等，则AB=AD；

根据全等三角形的判定定理、题目中的条件和结论：两组角及其夹边分别相等的两个三角形全等，∠BAE=∠DAF，AB=AD，∠B=∠ADF，则△BAE≌△DAF；

根据全等三角形的性质定理和结论：全等三角形的对应边相等，△BAE≌△DAF，则BE＝DF，AE=AF。

2、证明：BE＋DG＝EG

根据角平分线的性质定理和题目中的条件：角平分线可以得到两个相等的角，AG为∠EAF的平分线，则∠EAG=∠FAG；

根据全等三角形的判定定理、题目中的条件和结论：两组边及其夹角分别相等的两个三角形全等，AE=AF，∠EAG=∠FAG，AG=AG，则△EAG≌△FAG；

根据全等三角形的性质定理和结论：全等三角形的对应边相等，△EAG≌△FAG，则EG＝FG。

根据题目中的条件和结论：DF+DG=FG，BE＝DF，EG＝FG，则BE＋DG＝EG。

3、当∠EAF＝45°，证明：DF＋EF＝BE

添加辅助线分析：根据需要证明的结论：DF＋EF＝BE，考虑要把三条线段移到一起才能找相互之间的数量关系，所以，利用全等三角形的性质：全等三角形的对应边相等，把DF、EF进行等量转换，转移到BE上面，就得到需要证明的结论。所以，这样添加辅助线：在BC上取一点G，使得BG=DF。

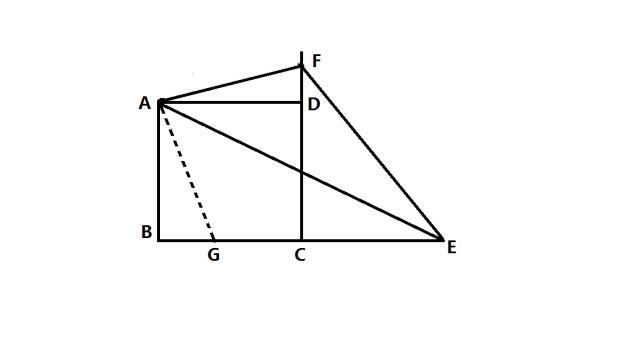
根据全等三角形的判定定理、辅助线和结论：两组边及其夹角分别相等的两个三角形全等，AB=AD，∠ABG=∠ADF，BG=DF，则△ABG≌△ADF；

根据全等三角形的性质定理和结论：全等三角形的对应边相等，对应角相等，△ABG≌△ADF，则AG＝AF，∠BAG=∠DAF；

根据题目中的条件和结论：∠BAG=∠DAF，∠EAF＝∠DAF+∠EAD，∠EAF＝45°，则∠BAG +∠EAD＝45°；

根据题目中的条件：正方形的四个角为直角，则∠BAD=90°；

根据题目中的条件和结论：∠BAD=90°，∠BAD=∠BAG+∠GAE+∠EAD，∠BAG +∠EAD＝45°，∠GAE=45°；

根据题目中的条件和结论：∠EAF＝45°，∠GAE=45°，则∠GAE=∠EAF；

根据全等三角形的判定定理、辅助线和结论：两组边及其夹角分别相等的两个三角形全等，AG＝AF，∠GAE=∠EAF，AE=AE，则△GAE≌△EAF；

根据全等三角形的性质定理和结论：全等三角形的对应边相等，对应角相等，△GAE≌△EAF，则EG＝EF；

根据辅助线和结论：BG=DF，EG＝EF，BG+EG= BE，则DF＋EF＝BE。

结语

关于全等三角形的几何证明题解题思路分为以下几步：

第一、从条件出发，推理得到相关的结论

对于较为简单的几何证明题，直接从条件出发，就可以推论得到题目需要证明的结论。特别注意：根据定理进行推论时，必须具备定理中要求的所有条件，才能进行正确地推理。

第二、从结论出发，反推需要先得到哪些条件

对于较为复杂的几何证明题，不仅需要从条件出发推理结论，还需要从结论出发反推需要先得到哪些条件，通过双向推理，就能得到题目需要证明的结论。

第三、根据题意，合理添加辅助线帮助解题

根据题目中的条件和结论，如果直接推理得不到需要的结论，就要考虑添加辅助线来帮助证明，一般考虑构造全等三角形，把线段、角进行等量转换，就能得到需要证明的结论。

总之，只有熟练掌握几何证明题的正确解题思路，并灵活运用全等三角形的判定和性质定理，才能成功应对这类题型，为数学期末考试取得高分加油助力！