数形结合: 数形结合的思想方法是数学教学内容的主线之一，应用数形结合的思想，可以解决函数问题：借助于图象研究函数的性质是一种常用的方法。函数图象的几何特征与数量特征紧密结合，体现了数形结合的特征与方法。
一般在函数f(x)中包含两种函数(指数函数，对数函数，二次函数等)
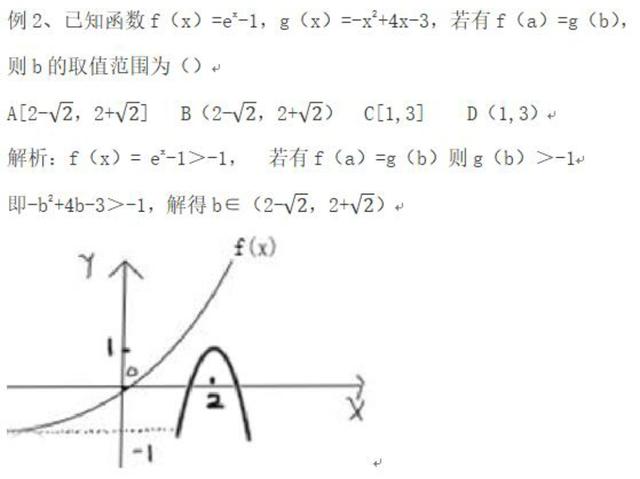
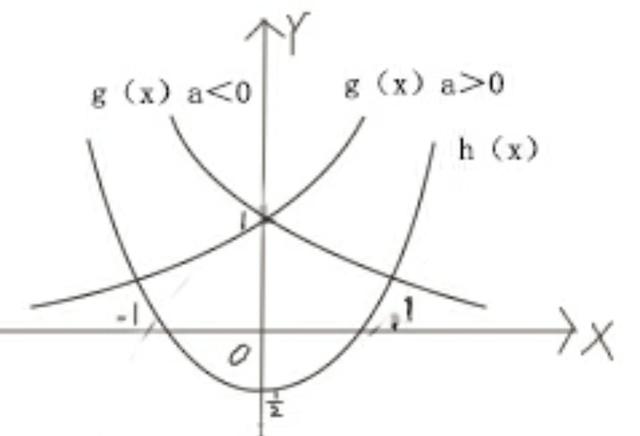
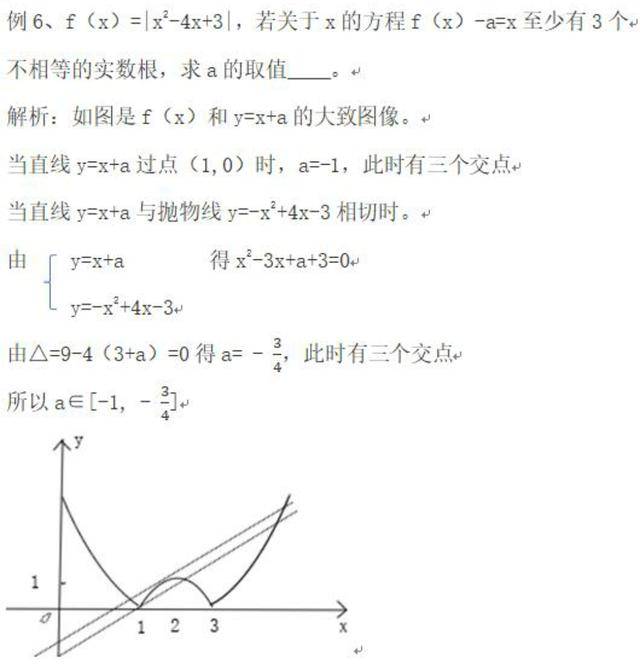
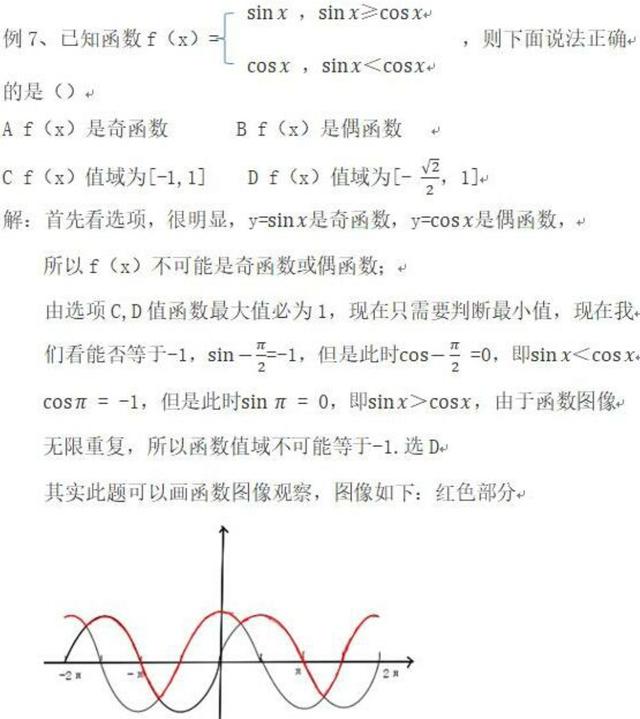
如f(x)=a^x+x^2 ，此函数包含y=a^x与y=x^2(指数函数和二次函数)，像这里f(x)这种形式的函数可以分成两个函数画图，观察它们的交点情况求参数范围或求其根的情况
上一篇 : 函数：第十一节：构造函数解题思路
下一篇 : 函数：第十三节，复合函数求零点，数形结合
加载中,请稍侯......
精彩评论