高考数学试题+完美解析！永久收藏！

全国新课标II卷试题+解析

一.选择题：本题共12道，每小题5分，共60分。在每小题给出的四个选项中，只有一个项是符合题目要求的。

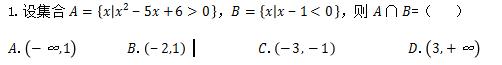
【解析】考察一元二次不等式，一元一次不等式的解法，集合的运算

【解析】考察复数的共轭，及其坐标表示

【解析】考察向量的坐标运算，向量的减法，求模，数量积等基本公式，此题只要依题意进行公式套入即可。

【解析】考察统计中各个数据的含义，此题需理解中位数的求法即可。

【详解】9个数的中位数去掉两端的两个数据后，新7个数的中位数和原来相同，故选A

【解析】此题看似不等式，实则是考察函数的单调性，通过函数单调性比较函数值的大小关系。

【解析】此题考察面面平行的判定定理。

【详解】判定定理：如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行，那么这两个平面平行。故选B

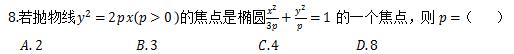
【解析】圆锥曲线，考察抛物线和椭圆的焦点坐标，代入焦点坐标公式中即可求解，难度中等。注意识别焦点位置。

【解析】考察图像变换中的含绝对值的图像变换，则利用图像判断函数单调区间

【解析】考察三角函数的恒等变换，利用二倍角公式，可化简求tanα，进而求sinα

【解析】此题考察双曲线的离心率的求法，根据题意做出图像，已知条件中的PQ=OF ，寻找关于a，b，c的等量关系，变形整理出离心率，是难题

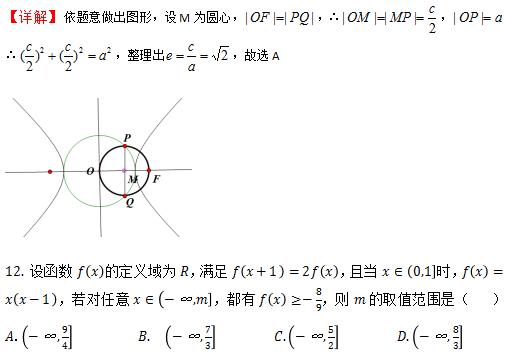
【解析】此题是“类周期函数”函数每向右一个单位，纵坐标总扩大2倍，做出函数图像，解出相应的函数解析式，再根据恒成立的条件，可求m的取值范围。

【解析】统计问题，考察频率分布中的平均值的求法，方法：频率乘相应数据再求和

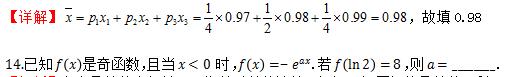
【解析】考察函数的奇偶性，及指数对数的计算。根据已知区间的函数值，利用奇函数性质转换到未知区间的函数值，可求参数a

【解析】此题考查解三角形中余弦定理，面积公式的应用。应用余弦定理课解出a和c，在用面积公式可解

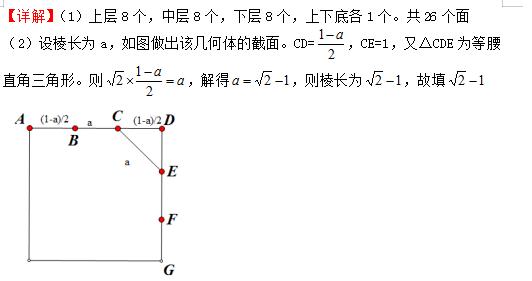
【解析】本题考察数学文化，注重社会主义核心价值观，并将5分拆成2+3分两部分，利于学生拿分；第一空，应用题中“对称”二字，可数出面数；第二空，恰当做出截面是关键，把立体图形的放在平面几何中研究，是解决立体几何的重要手段1

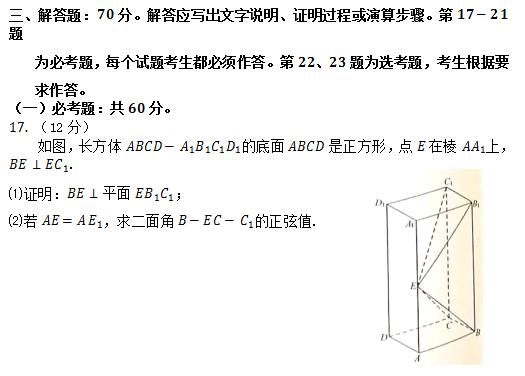
【解析】

（1）问考察线面垂直的判定定理，找到与BE垂直的两条相交直线

（2）问考察空间向量中二面角的求法，注意此题问的是正弦值，还需将余弦值转化为正弦值。

【解析】

独立事件的概率，也叫“积事件”，同时考察数学的应用能力，（1）问中x=2，说明甲得2分或者乙得2分。（2）问需分析好情况，4球后甲获胜的情况是双方打成11平后甲连赢2球。

【解析】

（1）考察证明数列是等比等差的方法，都是用定义法，即用后一项比（减）前一项等于常数；

（2）方程组法求通项公式；求第一问的通项公式后，解方程组即可；

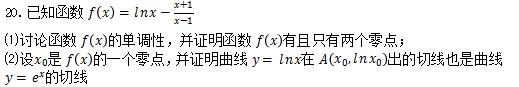
【解析】

（1）利用导数判断函数单调性，零点存在定理的应用

（2）设而不求的的思想应用极值点，未知切点的切线方程的求法。此题是难题

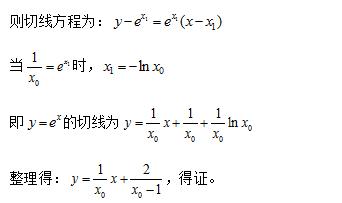
【解析】

（1）求轨迹方程，通过已知条件的斜率之积为定值，可整理出x，y的关系式，即可

（2）利用斜率之积为-1证明直角三角形；利用几何关系的转化，将△PQG的面积转化到2倍△OQG的面积，利用弦长公式，点到直线距离表示面积，再利用均值不等式求出最值，此题运算量较大。

【解析】

（1）考察极坐标与直角坐标的转化

（2）极坐标在解析几何中的应用，利用极坐标表示P点直角坐标，利用垂直条件整理出P点轨迹方程

【解析】

（1）分类讨论解不等式；或利用分段函数图像解不等式；

（2）分类讨论处理含绝对值不等式恒成立问题，根据a≥1和a<1两种情况。