举一反三系列15一对等积三角形

如图1，在四边形ABCD中，对角线AC、BD相交于点O，如果AD∥BC，则△ABO与△CDO的面积相等．

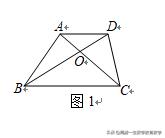
这个结论证明非常容易：

因为AD∥BC，所以A、D到BC的距离相等，

又因为△ABC与△DBC有公共的底边BC，

所以△ABC与△DBC的面积相等，

把它们的面积同时减去△OBC的面积，得

△ABO与△CDO的面积相等．

运用这个简单的结论解决有关面积问题十分简单．请看：

例 如图2，正方形ABCD和EFGC中，正方形EFGC的边长为1，用a的代数式表示阴影部分△AEG的面积为__________.

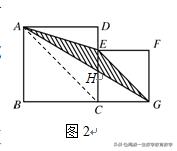
解析：连结AC．则易知AC∥EG．设AG交CE于H，则有上述结论，得：

△AEH的面积等于△CGH的面积，

从而阴影部分△AEG的面积

＝△AEH的面积＋△GEH的面积

＝△CGH的面积＋△GEH的面积

＝△CEG的面积

＝1/2×正方形EFGC的面积＝1/2．

练习：

（1）如图3，菱形ABCD和菱形ECGF的边长分别为2和3，∠A＝120°，则图中阴影部分的面积是（ ）

A．√3 B．2 C．3 D．√2

（答案：A）

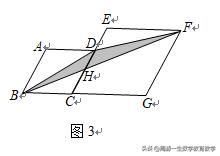
（2）如图4，已知四边形ABCD，在BC延长线上求作一点E，使△ABE的面积与四边形ABCD的面积相等．

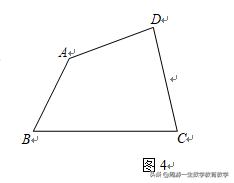
（提示：连接AC，过点D作AC的平行线）

(3) 如图1，在四边形ABCD中，AD∥BC，对角线AC、BD相交于点O，如果四边形ABCD的面积为S，△AOB的面积为2S/9，求AD/BC的值.

（答案：1/2）