例题

如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．

（1）求证：四边形DEGF是平行四边形；

（2）当点G是BC的中点时，求证：四边形DEGF是菱形．

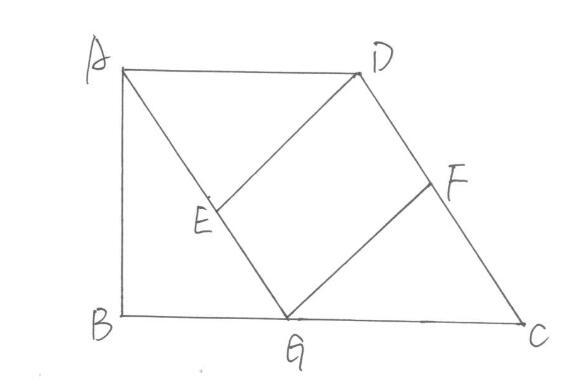
1、证明四边形DEGF是平行四边形

根据平行四边形的判定和题目中的条件：两组对边分别平行的四边形是平行四边形，AD∥BC，AG∥CD，则四边形ADCG是平行四边形。

根据平行四边形的性质和结论：平行四边形的两组对边分别相等，四边形ADCG是平行四边形，则AG=CD；

根据题目中的条件：点E、F分别为AG、CD的中点，则EG=AG/2，DF=DC/2；

根据结论：AG=CD，EG=AG/2，DF=DC/2，则EG=DF；

根据平行四边形的判定，题目中的条件和结论：一组对边平行且相等的四边形为平行四边形，AG∥CD，EG=DF，则四边形DEGF是平行四边形。

2、当点G是BC的中点时，证明四边形DEGF是菱形

根据前一题的结论：四边形DEGF是平行四边形，则需要证明结论必须先证明一组邻边相等；根据题目中的条件：F是DC的中点，∠B=90°，则考虑添加辅助线构造直角三角形，利用直角三角形斜边中线定理，得到平行四边形的一组邻边相等，则证得需要证明的结论。所以，这样添加辅助线：连接DG。

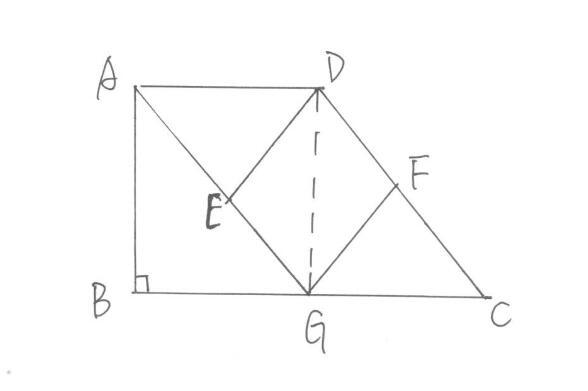
根据平行四边形的性质和结论：平行四边形的两组对边分别相等，四边形ADCG是平行四边形，则AD=GC；

根据题目中的条件：点G是BC的中点，则BG=CG；

根据结论：AD=GC，BG=CG，则AD=BG；

根据平行四边形的判定、题目中的条件和结论：一组对边平行且相等的四边形为平行四边形，AD∥BC，AD=BG，则四边形ADGB为平行四边形。

根据平行四边形的性质和结论：平行四边形的两组对边分别平行，四边形ADGB为平行四边形，则AB∥DG；

根据平行线的性质和题目中的条件：两直线平行同位角相等，AB∥DG，∠B=90°，则∠DGC=∠B=90°，即△DGC为直角三角形；

根据直角三角形斜边中线定理、题目中的条件和结论：直角三角形斜边上的中线等于斜边的一半，△DGC为直角三角形，点G是BC的中点，则FG=DC/2=DF；

根据菱形的判定、题目中的结论：一组邻边相等的平行四边形为菱形，四边形DEGF是平行四边形，FG= DF，则四边形DEGF是菱形。

结语：

特殊四边形的证明题解题思路有以下几个重点：

第一、合理选择判定定理

根据题目中的条件与特殊四边形边、角或对角线的关系，选择恰当的判定定理，利用条件先证明得到判定定理成立需要的所有条件，从而证明得到特殊四边形。

第二、灵活运用判定定理

证明特殊四边形的过程中，可以一步到位直接证明到结论；也可以分步进行证明，比如需要证明矩形，可以先证明到平行四边形，再证明到一个角为直角，则这样的四边形为矩形。

第三、充分利用性质定理

证明得到特殊四边形以后，根据性质定理可以得到四边形的边、角、对角线之间的数量与位置关系，为进一步证明其他结论创造条件。

总之，只有理清特殊四边形的相关知识点之间的关系，才能灵活运用判定、性质定理，成功应对这一类题型，为期末考试取得高分加油助力！